Conceção e validação de um instrumento para a observação de aulas de matemática no ensino secundário: grupo nominal e método Delphi
DOI:
https://doi.org/10.30827/relieve.v27i2.21812Palavras-chave:
método Delphi, grupo nominal, ensino da matemática, ensino secundário, instrumento de observaçãoResumo
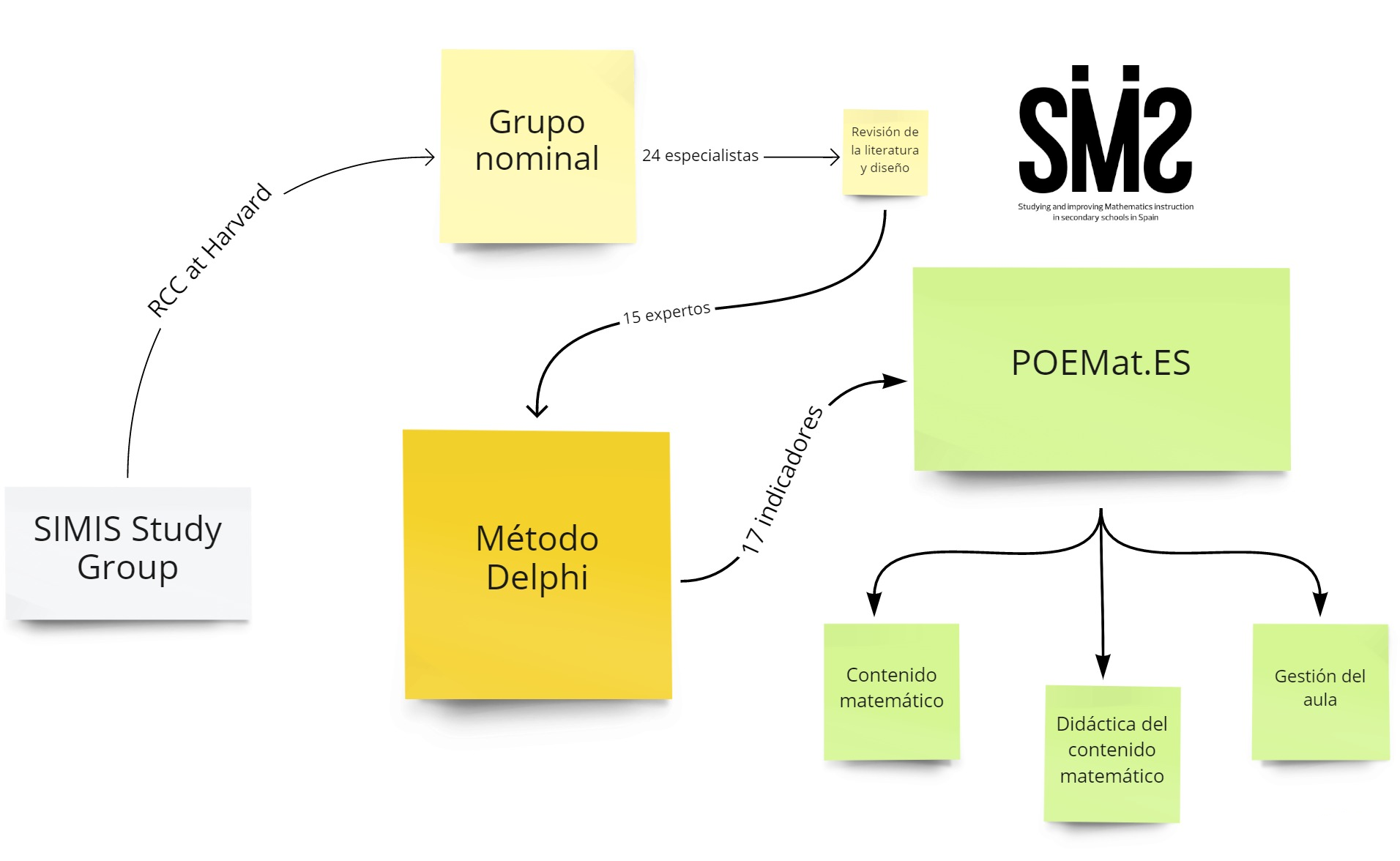
O uso dos processos de observação e interpretação da prática docente como ferramenta de aprendizagem para os docentes é raro em Espanha. Para promover a sua utilização, considera-se importante dispor de instrumentos que facilitem esta análise da prática, refletindo, ao mesmo tempo, as características particulares do contexto educativo em que são utilizados. Este estudo apresenta o processo de conceção, construção e validação do POEMat.ES, um instrumento de observação e interpretação da prática docente nas aulas de matemática a nível do ensino secundário. Este processo consiste em duas fases: 1) revisão da literatura e conceção, utilizando um grupo nominal com 24 especialistas; 2) construção e validação utilizando um método Delphi em duas fases, com 15 especialistas. A versão final do instrumento está organizada em três dimensões: conteúdo matemático, didática do conteúdo matemático e gestão da aula, com um total de 17 indicadores, classificando-se cada um deles em quatro níveis. As metodologias de consenso utilizadas são consideradas adequadas para a escolha e validação dos indicadores que enquadram a observação da prática docente. Conclui-se que a POEMat.ES é um instrumento útil para sistematizar a observação da prática docente e, assim, compreender e interpretar com precisão o processo de ensino da matemática na aula de matemática do ensino secundário na realidade espanhola.
Downloads
Referências
Aguilar-González, A., Muñoz-Catalán, M.C., Carrillo-Yáñez, J., & Rodríguez-Muñiz, L. J. (2018). ¿Cómo establecer relaciones entre conocimiento especializado y concepciones del profesorado de matemáticas? PNA, 13(1), 41-61. http://dx.doi.org/10.30827/pna.v13i1.7944
Barriendos, A., Berger, B., Domínguez, E., & Martínez, M. V. (2018). Manual PROMATE. Pauta de observación de clases de matemáticas impartidas por profesores principiantes. Centro de Investigación Avanzada en Educación de Chile.
Bostic, J., Lesseig, K., Sherman, M., & Boston, M. (2021). Classroom observation and mathematics education research. Journal of Mathematics Teacher Education, 24, 5–31. https://doi.org/10.1007/s10857-019-09445-0
Boston, M.D., & Candela, A.G. (2018). The Instructional Quality Assessment as a tool for reflecting on instructional practice. ZDM Mathematics Education, 50(3), 427-444. https://doi.org/10.1007/s11858-018-0916-6
Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Libros del Zorzal.
Buck, A. J., Gross, M., Hakim, S., & Weinblatt, J. (1993). Using the Delphi process to analyze social policy implementation: A post hoc case from vocational rehabilitation. Policy Sciences, 26, 271-288. https://doi.org/10.1007/BF00999473
Cabero, J. (2014). Formación del profesorado universitario en TIC. Aplicación del método Delphi para la selección de los contenidos formativos. Educación XX1, 17(1), 111-132. https://doi.org/10.5944/educxx1.17.1.10707
Cabero, J., & Barroso, J. (2013). La utilización del juicio de experto para la evaluación de TIC: el coeficiente de competencia experta. Bordón. Revista de Pedagogía, 65(2), 25-38. https://doi.org/10.13042/brp.2013.65202
Cabero, J., & Infante, A. (2014). Empleo del método Delphi y su empleo en la investigación en comunicación y educación. EDUTEC. Revista electrónica de tecnología educativa, 48, a272-a272. https://doi.org/10.21556/edutec.2014.48.187
Cabero, J., & Llorente, M. C. (2013). La aplicación del juicio de experto como técnica de evaluación de las tecnologías de la información y comunicación (TIC). Revista de Tecnología de Información y Comunicación en Educación, 7(2), 11-22.
Charalambous, C.Y., & Praetorius, A.K. (2018). Studying mathematics instruction through different lenses: setting the ground for understanding instructional quality more comprehensively. ZDM Mathematics Education, 50(3), 355–366. https://doi.org/10.1007/s11858-018-0914-8
Clayton, M. J. (1997). Delphi: a technique to harness expert opinion for critical decision‐making tasks in education. Educational psychology, 17(4), 373-386. https://doi.org/10.1080/0144341970170401
Diego-Mantecón, J. M., & Córdoba-Gómez, F. J. (2019). Adaptación y validación del MRBQ (Mathematics-Related Beliefs Questionnaire) al contexto colombiano con estudiantes de secundaria. Educación matemática, 31(1), 66-91. https://doi.org/10.24844/em3101.03
Dolores, C., & Ibáñez, G. (2020). Conceptualizaciones de la Pendiente en Libros de Texto de Matemáticas. Bolema: Boletim de Educação Matemática, 34, 825-846. https://doi.org/10.1590/1980-4415v34n67a22
Duval, R. (1993). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En E. Hitt (Ed.), Investigaciones en Matemática Educativa II (pp. 173-201). Grupo Editorial Iberoamérica.
Eccius-Wellmann, C., Lara-Barragán, A. G., Martschink, B., & Freitag, S. (2017). Comparación de perfiles de ansiedad matemática entre estudiantes mexicanos y estudiantes alemanes. Revista iberoamericana de educación superior, 8(23), 69-83. https://doi.org/10.22201/iisue.20072872e.2017.23.246
Garzón, D. (2017). Análisis de las decisiones del profesor de matemáticas en su gestión de aula. Revista Educación Matemática, 29(3), 131-160. https://doi.org/10.24844/EM2903.05
Gordon, T. J. (1994). The Delphi method. In J.C. Glenn & T.J. Gordon (Eds.). Futures Research Methodology Version 2.0. (CD-Rom). American Council for the United Nations University.
Hill, H., Blunk, M.L., Charalambous, C.Y., Lewis, J.M., Phelps, G.C., Sleep, L., & Ball, D. (2008). Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study. Routledge Cognition and Instruction, 26(4). https://doi.org/10.1080/07370000802177235
Kaiser, G. (2020) Mathematical Modelling and Applications in Education. In S. Lerman (Eds.), Encyclopedia of Mathematics Education. Springer. https://doi.org/10.1007/978-3-030-15789-0_101
Landeta, J. (1999). El método Delphi. Una técnica de previsión para la incertidumbre. Ariel.
Linstone, H. A., & Turoff, M. (1975). The delphi method. Addison-Wesley.
Liu, R. D., Wang, J., Star, J. R., Zhen, R., Jiang, R. H., & Fu, X. C. (2018). Turning potential flexibility into flexible performance: Moderating effect of self-efficacy and use of flexible cognition. Frontiers in psychology, 9, 646. https://doi.org/10.3389/fpsyg.2018.00646
Llorente, L. (2013). Assessing Personal Learning Environments (PLEs). An expert evaluation. Journal of New Approaches in Educational Research), 2(1), 39-44. https://doi.org/10.7821/naer.2.1.39-44
López-Gómez, E. (2018). El método Delphi en la investigación actual en educación: una revisión teórica y metodológica. Educación XX1, 21(1), 17-40. https://doi.org/10.5944/educXX1.20169
Ludwig, B. (1997). Predicting the future: Have you considered using the Delphi methodology. Journal of extension, 35(5), 1-4.
Martínez, A. (1988). Diseños experimentales: métodos y elementos de teoría. Trillas.
Martino, J. (1999). Thirty years of change and stability. Technological Forecasting and Social Change, 62(1-2), 13-18. https://doi.org/10.1016/S0040-1625(99)00011-6
Martins, G. A., & Theóphilo, C. R. (2007). Metodologia da Investigação Científica para Ciências Sociais Aplicadas. Atlas
Matsumura, L. C., Garnier, H., Slater, S. C., & Boston, M. (2008). Toward measuring instructional interactions ‘at-scale’. Educational Assessment, 13(4), 267–300. https://doi.org/10.1080/10627190802602541
Maz-Machado, A., Madrid, M. J., León-Mantero, C., & Jiménez-Fanjul, N. (2019). Mathematical practical sessions with manipulatives: Trainee teachers’ perceptions of their utility. South African Journal of Education, 39(2), Art. #1620. https://doi.org/10.15700/saje.v39ns2a1620
McMillan, S.S., King, M., & Tully, M.P. (2016). How to use the nominal group and Delphi techniques. International Journal of Clinic Pharmacy, 38, 655–662. https://doi.org/10.1007/s11096-016-0257-x
Mengual, S., Roig, R., & Mira, J.B. (2016). Delphi study for the design and validation of a questionnaire about digital competences in higher education. International Journal of Educational Technology in High Education, 13, 12. https://doi.org/10.1186/s41239-016-0009-y
Molina, O., & Samper, C. (2019). Tipos de problemas que provocan la generación de argumentos inductivos, abductivos y deductivos. Bolema: Boletim de Educação Matemática, 33, 109-134. https://doi.org/10.1590/1980-4415v33n63a06
Moore, C. M. (1987). Group techniques for idea building. Sage Publications, Inc.
Novakowski, N., & Wellar, B. (2008). Using the Delphi technique in normative planning research: methodological design considerations. Environment and Planning A, 40(6), 1485-1500. https://doi.org/10.1068/a39267
Okoli, C., & Pawlowski, S. D. (2004). The Delphi method as a research tool: an example, design considerations and applications. Information & management, 42(1), 15-29. https://doi.org/10.1016/j.im.2003.11.002
Openshaw, R., & Walshaw, M. (2019). Transnational Synergies in School Mathematics and Science Debates. Springer Nature. https://doi.org/10.1007/978-3-030-28269-1
Orton, A. (2003). Didáctica de las matemáticas. Ministerio de Educación, Cultura y Deporte-Ediciones Morata.
Parenté, F. J., & Anderson, J.K. (1987). Delphi inquiry systems. En G. Wright & P. Ayton (Eds.), Judgemental Forecasting (pp. 129-156). John Wiley.
Patton, M. (1990). Qualitative evaluation and research methods. Newbury Park, CA.
Piburn, M., & Sawada, D. (2000). Reformed teaching observation protocol (RTOP): Reference manual. Technical Report. Arizona Collaborative for Excellence in the Preparation of Teachers.
Planas, N., Arnal-Bailera, A., & García-Honrado, I. (2018). El discurso matemático del profesor: ¿Cómo se produce en clase y cómo se puede investigar? Enseñanza de las Ciencias, 36(1), 45-60. https://doi.org/10.5565/rev/ensciencias.2240
Praetorius, A. K., & Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: looking back and looking forward. ZDM Mathematics Education, 50(3), 535-553. https://doi.org/10.1007/s11858-018-0946-0
Rodríguez, J.M., & Ruiz, J. (2019). El clima social en centros educativos: percepción del profesorado de Educación Secundaria Obligatoria de la Comunidad de Madrid. Revista de Investigación Educativa, 37(1), 231-250. https://doi.org/10.6018/rie.37.1.320541
Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Transformation: Using examples in mathematics teaching. In Developing Primary Mathematics Teaching: Reflecting on Practice with the Knowledge Quartet (pp. 67-100). SAGE Publications. https://doi.org/10.4135/9781446279571
Schlesinger, L., & Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Mathematics Education, 48, 29–40. https://doi.org/10.1007/s11858-016-0765-0
Schneider, M., Rittle-Johnson, B., & Star, J. R. (2011). Relations between conceptual knowledge, procedural knowledge, and procedural flexibility in two samples differing in prior knowledge. Developmental Psychology, 47(6), 1525-1538. https://doi.org/10.1037/a0024997
Shah, H., & Kalaian, S. A. (2009). Which Parametric Statistical Method to Use For Analyzing Delphi Data? Journal of Modern Applied Statistical Method, 8(1), 226-232. https://doi.org/10.22237/jmasm/1241137140
Teddlie, C., Creemers, B., Kyriakides, L., Muijs, D., & Yu, F. (2006). The international system for teacher observation and feedback: Evolution of an international study of teacher effectiveness constructs. Educational Research and Evaluation, 12(6), 561–582. https://doi.org/10.1080/13803610600874067
Thomas, C. A., & Berry III, R. Q. (2019). A Qualitative Metasynthesis of Culturally Relevant Pedagogy & Culturally Responsive Teaching: Unpacking Mathematics Teaching Practices. Journal of Mathematics Education at Teachers College, 10(1), 21-30. https://doi.org/10.7916/jmetc.v10i1.1668
Thompson, C. J., & Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: Improving design and rigour. Mathematics Education Research Journal, 26(2), 301–323. https://doi.org/10.1007/s13394-013-0099-y
van den Ham, A. K., & Heinze, A. (2018). Does the textbook matter? Longitudinal effects of textbook choice on primary school students’ achievement in mathematics. Studies in Educational Evaluation, 59, 133-140. https://doi.org/10.1016/j.stueduc.2018.07.005
Van Zoest, L. R., Peterson, B. E., Rougée, A. O., Stockero, S. L., Leatham, K. R., & Freeburn, B. (2021). Conceptualizing important facets of teacher responses to student mathematical thinking. International Journal of Mathematical Education in Science and Technology, 1-26. https://doi.org/10.1080/0020739X.2021.1895341
Vergnaud, G. (2013). Pourquoi la théorie des champs conceptuels? Infancia y Aprendizaje, 36(2), 131-161. https://doi.org/10.1174/021037013806196283
von der Gracht, H.A. (2012). Consensus measurement in Delphi studies: review and implications for future quality assurance. Technological Forecasting and Social Change, 79(8), 1525-1536. https://doi.org/10.1016/j.techfore.2012.04.013
Walkowiak, T. A., Berry, R. Q., Meyer, J. P., Rimm-Kaufman, S. E., & Ottmar, E. R. (2014). Introducing an observational measure of standards-based mathematics teaching practices: Evidence of validity and score reliability. Educational Studies in Mathematics, 85(1), 109–128. https://doi.org/10.1007/s10649-013-9499-x
Weber, K. E., Gold, B., Prilop, C. N., & Kleinknecht, M. (2018). Promoting pre-service teachers' professional vision of classroom management during practical school training: Effects of a structured online-and video-based self-reflection and feedback intervention. Teaching and Teacher Education, 76, 39-49. https://doi.org/10.1016/j.tate.2018.08.008
Downloads
Publicado
Como Citar
Edição
Secção
Licença
Direitos de Autor (c) 2021 RELIEVE - Revista Electrónica de Investigación y Evaluación Educativa

Este trabalho encontra-se publicado com a Creative Commons Atribuição-NãoComercial 4.0.
Los autores ceden de forma no exclusiva los derechos de explotación de los trabajos publicados a RELIEVE (a los solos efectos de favorecer la difusión de los artículos publicados:firmar contratos de difusión, de integración en bases de datos, etc.) y consienten que se distribuyan bajo la licencia de Creative Commons Reconocimiento-Uso No Comercial 4.0 International (CC-BY-NC 4.0), que permite a terceros el uso de lo publicado siempre que se mencione la autoría de la obra y la fuente de publicación, y se haga uso sin fines comerciales.
Los autores pueden llegar a otros acuerdos contractuales adicionales e independientes, para la distribución no exclusiva de la versión del trabajo publicado en esta revista (por ejemplo, incluyéndolo en un repositorio institucional o publicándolo en un libro), siempre y cuando se cite claramente que la fuente original de publicación es esta revista.
La mera remisión del artículo a RELIEVE supone la aceptación de estas condiciones.













