Diseño y validación de un instrumento para observación de clases de matemáticas en Educación Secundaria: grupo nominal y método Delphi

Blanca Arteaga-Martínez; Jesús Macías-Sánchez; Marta Pla-Castells; Mónica Ramírez-García

doi:10.30827/relieve.v27i2.21812

Authors

Blanca Arteaga-Martínez Universidad Nacional de Educación a Distancia (UNED)
Jesús Macías-Sánchez Universidad Complutense de Madrid
Marta Pla-Castells Universitat de València
Mónica Ramírez-García Centro Universitario La Salle

DOI:

https://doi.org/10.30827/relieve.v27i2.21812

Keywords:

Delphi method, expert panel, mathematics teaching, secondary teaching, observation tool

Abstract

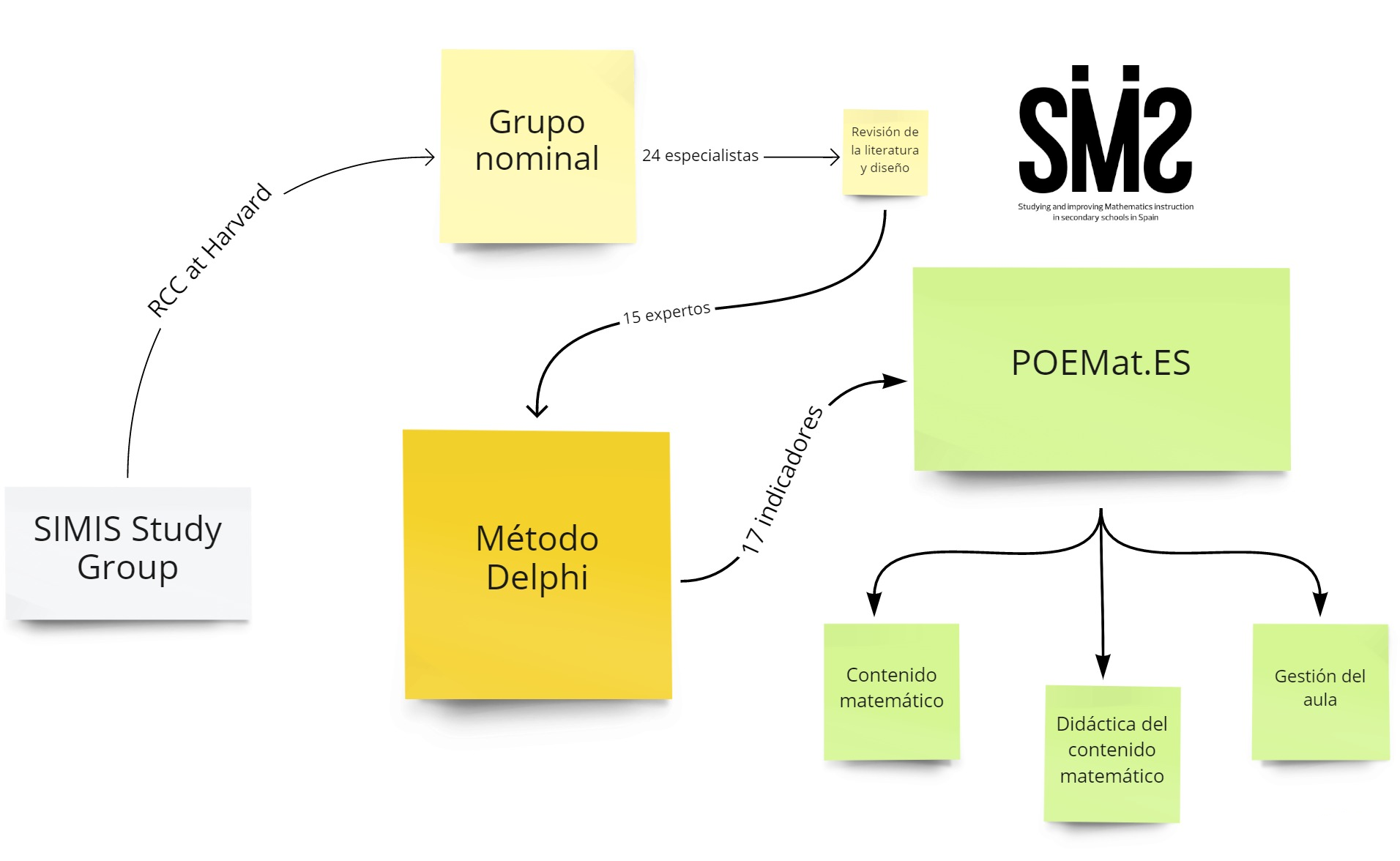
Observation and interpretation processes are rarely used in teaching practice as learning tools in Spain. In order to encourage their use, it is important to have instruments that facilitate analysis in practice and that gather information about the particular characteristics of the educational context in which they are used. The present study presents the process of design, construction and validation of POEMat.ES, an observation and interpretation instrument for use in relation to the teaching of secondary education mathematics classes. This process consisted of two phases: 1) literature review and design using an expert panel made up of 24 specialists; 2) construction and validation via the Delphi method conducted by 15 experts over two rounds. The final version of the tool was organized around three dimensions: mathematical content, didactics of mathematical content and classroom management. It comprised 17 indicators, each of which was classified according to four levels. The methodology applied conformed to consensus, with this being considered adequate for the selection and validation of the indicators that frame the observation of teaching practice. I can be concluded that POEMat.ES is a useful tool for systematizing the observation of teaching practice in order to understand and accurately interpret the process of teaching mathematics in secondary education in the Spanish context.

Downloads

Download data is not yet available.

Author Biographies

Blanca Arteaga-Martínez, Universidad Nacional de Educación a Distancia (UNED)

Blanca Arteaga has a Degree in Mathematics (Universidad Autónoma de Madrid) and PhD in Education (Universidad Complutense de Madrid). Dr. Arteaga has combined her work as primary and secondary teacher with university lecturing (Universidad Carlos III de Madrid, Saint Louis University in Madrid, Universidad Internacional de La Rioja, Universidad de Alcalá and Universidad Rey Juan Carlos), research and project management. She is currently Assistant Professor at the Universidad Nacional de Educación a Distancia (UNED). Her research has focused on action-research in the classroom, with the didactics of mathematics as the backbone. In that areaa, she has managed and participated in several funded research projects and educational innovation projects with different universities and school networks. Dr. Arteaga is a member of the Adaptive Pedagogy research group at the Complutense University of Madrid.

Jesús Macías-Sánchez, Universidad Complutense de Madrid

Degree in Mathematics from the Universidad Complutense of Madrid, Master in Teacher Training and Master in Advanced Studies in Pedagogy from the Universidad Complutense of Madrid and PhD in Education from the Universidad Complutense of Madrid. He combines his work as a teacher at compulsory levels with teaching at university (Universidad Internacional de La Rioja, Universidad Europea de Madrid and Universidad Complutense of Madrid). Currently he is adjunct professor at the Universidad Complutense of Madrid (UCM) and teacher in compulsory education at the Colegio Brotmadrid. His research has focused on action research in the classroom, based on the teaching-learning process of mathematics. He has participated in some funded research projects and educational innovation projects.

Marta Pla-Castells, Universitat de València

Degree in Mathematics from Universitat de València (UVEG) and PhD in Computer Science from the same university. She has worked as director of European projects for the Institute of Robotics and ICT of the UVEG while she was associate professor in departments of the Faculty of Mathematics of the UVEG and the Universitat Jaume I of Castelló (UJI). At present she is a lecturer at UVEG. Due to her experience in software programming, she has been able to apply new technologies in the field of mathematics education. She has also worked in continuous training of primary school teachers in collaboration with the centre for training, innovation, and resources for teachers of the Valencian Regional Government. She currently belongs to the Mathematical Modelling research group at the Department of Didactics of Mathematics at the UVEG.

Mónica Ramírez-García, Centro Universitario La Salle

Degree in Mathematical Sciences, from the Universidad Autónoma de Madrid (Spain) in 1998 and PhD in Education from the Universidad Complutense of Madrid (Spain). She has worked as a professor at the Department of Experimental, Social and Mathematical Didactics in the Faculty of Education at the Universidad Complutense de Madrid (Spain) since 2011 and she currently works at the Centro Superior de Estudios Universitarios La Salle (Spain) since 2006. Her research interests have focused on the teaching-learning of mathematics in the early childhood education. In 2016, she started collaborating with several researchers from the Universidad de Sevilla and the Universidad de Huelva, applying the Mathematics Teachers Specialized Knowledge model (MTSK) both to her activity as a mathematics teacher educator and as a researcher.

References

Aguilar-González, A., Muñoz-Catalán, M.C., Carrillo-Yáñez, J., & Rodríguez-Muñiz, L. J. (2018). ¿Cómo establecer relaciones entre conocimiento especializado y concepciones del profesorado de matemáticas? PNA, 13(1), 41-61. http://dx.doi.org/10.30827/pna.v13i1.7944

Barriendos, A., Berger, B., Domínguez, E., & Martínez, M. V. (2018). Manual PROMATE. Pauta de observación de clases de matemáticas impartidas por profesores principiantes. Centro de Investigación Avanzada en Educación de Chile.

Bostic, J., Lesseig, K., Sherman, M., & Boston, M. (2021). Classroom observation and mathematics education research. Journal of Mathematics Teacher Education, 24, 5–31. https://doi.org/10.1007/s10857-019-09445-0

Boston, M.D., & Candela, A.G. (2018). The Instructional Quality Assessment as a tool for reflecting on instructional practice. ZDM Mathematics Education, 50(3), 427-444. https://doi.org/10.1007/s11858-018-0916-6

Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Libros del Zorzal.

Buck, A. J., Gross, M., Hakim, S., & Weinblatt, J. (1993). Using the Delphi process to analyze social policy implementation: A post hoc case from vocational rehabilitation. Policy Sciences, 26, 271-288. https://doi.org/10.1007/BF00999473

Cabero, J. (2014). Formación del profesorado universitario en TIC. Aplicación del método Delphi para la selección de los contenidos formativos. Educación XX1, 17(1), 111-132. https://doi.org/10.5944/educxx1.17.1.10707

Cabero, J., & Barroso, J. (2013). La utilización del juicio de experto para la evaluación de TIC: el coeficiente de competencia experta. Bordón. Revista de Pedagogía, 65(2), 25-38. https://doi.org/10.13042/brp.2013.65202

Cabero, J., & Infante, A. (2014). Empleo del método Delphi y su empleo en la investigación en comunicación y educación. EDUTEC. Revista electrónica de tecnología educativa, 48, a272-a272. https://doi.org/10.21556/edutec.2014.48.187

Cabero, J., & Llorente, M. C. (2013). La aplicación del juicio de experto como técnica de evaluación de las tecnologías de la información y comunicación (TIC). Revista de Tecnología de Información y Comunicación en Educación, 7(2), 11-22.

Charalambous, C.Y., & Praetorius, A.K. (2018). Studying mathematics instruction through different lenses: setting the ground for understanding instructional quality more comprehensively. ZDM Mathematics Education, 50(3), 355–366. https://doi.org/10.1007/s11858-018-0914-8

Clayton, M. J. (1997). Delphi: a technique to harness expert opinion for critical decision‐making tasks in education. Educational psychology, 17(4), 373-386. https://doi.org/10.1080/0144341970170401

Diego-Mantecón, J. M., & Córdoba-Gómez, F. J. (2019). Adaptación y validación del MRBQ (Mathematics-Related Beliefs Questionnaire) al contexto colombiano con estudiantes de secundaria. Educación matemática, 31(1), 66-91. https://doi.org/10.24844/em3101.03

Dolores, C., & Ibáñez, G. (2020). Conceptualizaciones de la Pendiente en Libros de Texto de Matemáticas. Bolema: Boletim de Educação Matemática, 34, 825-846. https://doi.org/10.1590/1980-4415v34n67a22

Duval, R. (1993). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En E. Hitt (Ed.), Investigaciones en Matemática Educativa II (pp. 173-201). Grupo Editorial Iberoamérica.

Eccius-Wellmann, C., Lara-Barragán, A. G., Martschink, B., & Freitag, S. (2017). Comparación de perfiles de ansiedad matemática entre estudiantes mexicanos y estudiantes alemanes. Revista iberoamericana de educación superior, 8(23), 69-83. https://doi.org/10.22201/iisue.20072872e.2017.23.246

Garzón, D. (2017). Análisis de las decisiones del profesor de matemáticas en su gestión de aula. Revista Educación Matemática, 29(3), 131-160. https://doi.org/10.24844/EM2903.05

Gordon, T. J. (1994). The Delphi method. In J.C. Glenn & T.J. Gordon (Eds.). Futures Research Methodology Version 2.0. (CD-Rom). American Council for the United Nations University.

Hill, H., Blunk, M.L., Charalambous, C.Y., Lewis, J.M., Phelps, G.C., Sleep, L., & Ball, D. (2008). Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study. Routledge Cognition and Instruction, 26(4). https://doi.org/10.1080/07370000802177235

Kaiser, G. (2020) Mathematical Modelling and Applications in Education. In S. Lerman (Eds.), Encyclopedia of Mathematics Education. Springer. https://doi.org/10.1007/978-3-030-15789-0_101

Landeta, J. (1999). El método Delphi. Una técnica de previsión para la incertidumbre. Ariel.

Linstone, H. A., & Turoff, M. (1975). The delphi method. Addison-Wesley.

Liu, R. D., Wang, J., Star, J. R., Zhen, R., Jiang, R. H., & Fu, X. C. (2018). Turning potential flexibility into flexible performance: Moderating effect of self-efficacy and use of flexible cognition. Frontiers in psychology, 9, 646. https://doi.org/10.3389/fpsyg.2018.00646

Llorente, L. (2013). Assessing Personal Learning Environments (PLEs). An expert evaluation. Journal of New Approaches in Educational Research), 2(1), 39-44. https://doi.org/10.7821/naer.2.1.39-44

López-Gómez, E. (2018). El método Delphi en la investigación actual en educación: una revisión teórica y metodológica. Educación XX1, 21(1), 17-40. https://doi.org/10.5944/educXX1.20169

Ludwig, B. (1997). Predicting the future: Have you considered using the Delphi methodology. Journal of extension, 35(5), 1-4.

Martínez, A. (1988). Diseños experimentales: métodos y elementos de teoría. Trillas.

Martino, J. (1999). Thirty years of change and stability. Technological Forecasting and Social Change, 62(1-2), 13-18. https://doi.org/10.1016/S0040-1625(99)00011-6

Martins, G. A., & Theóphilo, C. R. (2007). Metodologia da Investigação Científica para Ciências Sociais Aplicadas. Atlas

Matsumura, L. C., Garnier, H., Slater, S. C., & Boston, M. (2008). Toward measuring instructional interactions ‘at-scale’. Educational Assessment, 13(4), 267–300. https://doi.org/10.1080/10627190802602541

Maz-Machado, A., Madrid, M. J., León-Mantero, C., & Jiménez-Fanjul, N. (2019). Mathematical practical sessions with manipulatives: Trainee teachers’ perceptions of their utility. South African Journal of Education, 39(2), Art. #1620. https://doi.org/10.15700/saje.v39ns2a1620

McMillan, S.S., King, M., & Tully, M.P. (2016). How to use the nominal group and Delphi techniques. International Journal of Clinic Pharmacy, 38, 655–662. https://doi.org/10.1007/s11096-016-0257-x

Mengual, S., Roig, R., & Mira, J.B. (2016). Delphi study for the design and validation of a questionnaire about digital competences in higher education. International Journal of Educational Technology in High Education, 13, 12. https://doi.org/10.1186/s41239-016-0009-y

Molina, O., & Samper, C. (2019). Tipos de problemas que provocan la generación de argumentos inductivos, abductivos y deductivos. Bolema: Boletim de Educação Matemática, 33, 109-134. https://doi.org/10.1590/1980-4415v33n63a06

Moore, C. M. (1987). Group techniques for idea building. Sage Publications, Inc.

Novakowski, N., & Wellar, B. (2008). Using the Delphi technique in normative planning research: methodological design considerations. Environment and Planning A, 40(6), 1485-1500. https://doi.org/10.1068/a39267

Okoli, C., & Pawlowski, S. D. (2004). The Delphi method as a research tool: an example, design considerations and applications. Information & management, 42(1), 15-29. https://doi.org/10.1016/j.im.2003.11.002

Openshaw, R., & Walshaw, M. (2019). Transnational Synergies in School Mathematics and Science Debates. Springer Nature. https://doi.org/10.1007/978-3-030-28269-1

Orton, A. (2003). Didáctica de las matemáticas. Ministerio de Educación, Cultura y Deporte-Ediciones Morata.

Parenté, F. J., & Anderson, J.K. (1987). Delphi inquiry systems. En G. Wright & P. Ayton (Eds.), Judgemental Forecasting (pp. 129-156). John Wiley.

Patton, M. (1990). Qualitative evaluation and research methods. Newbury Park, CA.

Piburn, M., & Sawada, D. (2000). Reformed teaching observation protocol (RTOP): Reference manual. Technical Report. Arizona Collaborative for Excellence in the Preparation of Teachers.

Planas, N., Arnal-Bailera, A., & García-Honrado, I. (2018). El discurso matemático del profesor: ¿Cómo se produce en clase y cómo se puede investigar? Enseñanza de las Ciencias, 36(1), 45-60. https://doi.org/10.5565/rev/ensciencias.2240

Praetorius, A. K., & Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: looking back and looking forward. ZDM Mathematics Education, 50(3), 535-553. https://doi.org/10.1007/s11858-018-0946-0

Rodríguez, J.M., & Ruiz, J. (2019). El clima social en centros educativos: percepción del profesorado de Educación Secundaria Obligatoria de la Comunidad de Madrid. Revista de Investigación Educativa, 37(1), 231-250. https://doi.org/10.6018/rie.37.1.320541

Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Transformation: Using examples in mathematics teaching. In Developing Primary Mathematics Teaching: Reflecting on Practice with the Knowledge Quartet (pp. 67-100). SAGE Publications. https://doi.org/10.4135/9781446279571

Schlesinger, L., & Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Mathematics Education, 48, 29–40. https://doi.org/10.1007/s11858-016-0765-0

Schneider, M., Rittle-Johnson, B., & Star, J. R. (2011). Relations between conceptual knowledge, procedural knowledge, and procedural flexibility in two samples differing in prior knowledge. Developmental Psychology, 47(6), 1525-1538. https://doi.org/10.1037/a0024997

Shah, H., & Kalaian, S. A. (2009). Which Parametric Statistical Method to Use For Analyzing Delphi Data? Journal of Modern Applied Statistical Method, 8(1), 226-232. https://doi.org/10.22237/jmasm/1241137140

Teddlie, C., Creemers, B., Kyriakides, L., Muijs, D., & Yu, F. (2006). The international system for teacher observation and feedback: Evolution of an international study of teacher effectiveness constructs. Educational Research and Evaluation, 12(6), 561–582. https://doi.org/10.1080/13803610600874067

Thomas, C. A., & Berry III, R. Q. (2019). A Qualitative Metasynthesis of Culturally Relevant Pedagogy & Culturally Responsive Teaching: Unpacking Mathematics Teaching Practices. Journal of Mathematics Education at Teachers College, 10(1), 21-30. https://doi.org/10.7916/jmetc.v10i1.1668

Thompson, C. J., & Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: Improving design and rigour. Mathematics Education Research Journal, 26(2), 301–323. https://doi.org/10.1007/s13394-013-0099-y

van den Ham, A. K., & Heinze, A. (2018). Does the textbook matter? Longitudinal effects of textbook choice on primary school students’ achievement in mathematics. Studies in Educational Evaluation, 59, 133-140. https://doi.org/10.1016/j.stueduc.2018.07.005

Van Zoest, L. R., Peterson, B. E., Rougée, A. O., Stockero, S. L., Leatham, K. R., & Freeburn, B. (2021). Conceptualizing important facets of teacher responses to student mathematical thinking. International Journal of Mathematical Education in Science and Technology, 1-26. https://doi.org/10.1080/0020739X.2021.1895341

Vergnaud, G. (2013). Pourquoi la théorie des champs conceptuels? Infancia y Aprendizaje, 36(2), 131-161. https://doi.org/10.1174/021037013806196283

von der Gracht, H.A. (2012). Consensus measurement in Delphi studies: review and implications for future quality assurance. Technological Forecasting and Social Change, 79(8), 1525-1536. https://doi.org/10.1016/j.techfore.2012.04.013

Walkowiak, T. A., Berry, R. Q., Meyer, J. P., Rimm-Kaufman, S. E., & Ottmar, E. R. (2014). Introducing an observational measure of standards-based mathematics teaching practices: Evidence of validity and score reliability. Educational Studies in Mathematics, 85(1), 109–128. https://doi.org/10.1007/s10649-013-9499-x

Weber, K. E., Gold, B., Prilop, C. N., & Kleinknecht, M. (2018). Promoting pre-service teachers' professional vision of classroom management during practical school training: Effects of a structured online-and video-based self-reflection and feedback intervention. Teaching and Teacher Education, 76, 39-49. https://doi.org/10.1016/j.tate.2018.08.008