Diseño y validación de un instrumento para observación de clases de matemáticas en Educación Secundaria: grupo nominal y método Delphi
DOI:
https://doi.org/10.30827/relieve.v27i2.21812Palabras clave:
método Delphi, grupo nominal, enseñanza de las matemáticas, educación secundaria, instrumento de observaciónResumen
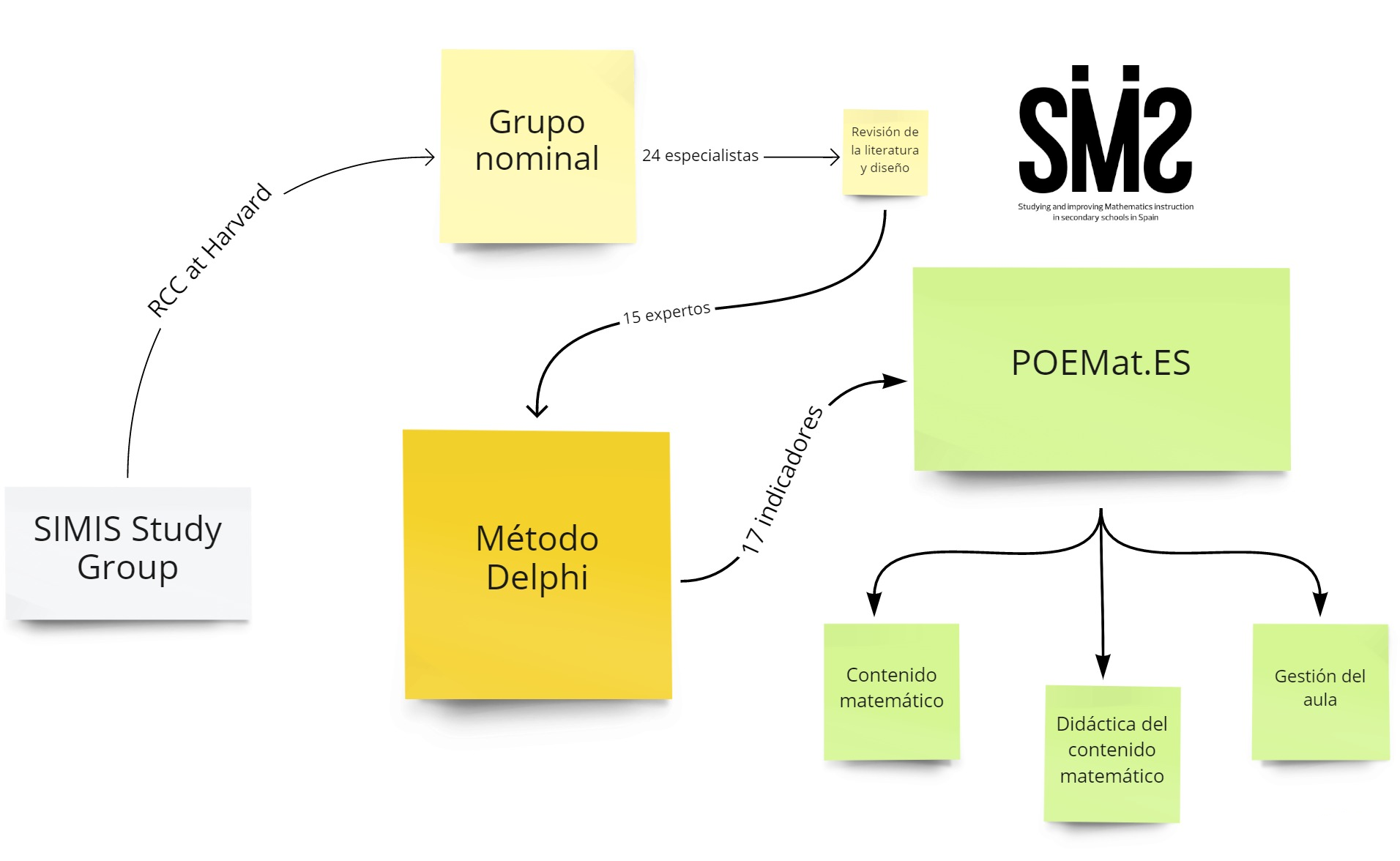
El uso de los procesos de observación e interpretación de la práctica docente como herramienta de aprendizaje para los docentes es infrecuente en España. Para promover su utilización, se considera la importancia de contar con instrumentos que faciliten este análisis de la práctica, a la vez que recogen las características particulares del contexto educativo donde se utilizan. Este estudio presenta el proceso de diseño, construcción y validación de POEMat.ES, un instrumento de observación e interpretación de la práctica docente, en las clases de matemáticas de la etapa de Educación Secundaria. Este proceso consta de dos fases: 1) revisión de la literatura y diseño, utilizando un grupo nominal con 24 especialistas; 2) construcción y validación mediante un método Delphi en dos rondas, con 15 expertos. La versión final del instrumento se organiza en torno a tres dimensiones: contenido matemático, didáctica del contenido matemático y gestión del aula, con un total de 17 indicadores, cada uno de los cuáles se clasifica en cuatro niveles. Las metodologías de consenso utilizadas se consideran adecuadas para la elección y validación de los indicadores que enmarcan la observación de la práctica docente. Se concluye que POEMat.ES es una herramienta útil para sistematizar la observación de la práctica docente y así comprender e interpretar con precisión el proceso de enseñanza de las matemáticas en el aula de matemáticas de Secundaria según la realidad española.
Descargas
Citas
Aguilar-González, A., Muñoz-Catalán, M.C., Carrillo-Yáñez, J., & Rodríguez-Muñiz, L. J. (2018). ¿Cómo establecer relaciones entre conocimiento especializado y concepciones del profesorado de matemáticas? PNA, 13(1), 41-61. http://dx.doi.org/10.30827/pna.v13i1.7944
Barriendos, A., Berger, B., Domínguez, E., & Martínez, M. V. (2018). Manual PROMATE. Pauta de observación de clases de matemáticas impartidas por profesores principiantes. Centro de Investigación Avanzada en Educación de Chile.
Bostic, J., Lesseig, K., Sherman, M., & Boston, M. (2021). Classroom observation and mathematics education research. Journal of Mathematics Teacher Education, 24, 5–31. https://doi.org/10.1007/s10857-019-09445-0
Boston, M.D., & Candela, A.G. (2018). The Instructional Quality Assessment as a tool for reflecting on instructional practice. ZDM Mathematics Education, 50(3), 427-444. https://doi.org/10.1007/s11858-018-0916-6
Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Libros del Zorzal.
Buck, A. J., Gross, M., Hakim, S., & Weinblatt, J. (1993). Using the Delphi process to analyze social policy implementation: A post hoc case from vocational rehabilitation. Policy Sciences, 26, 271-288. https://doi.org/10.1007/BF00999473
Cabero, J. (2014). Formación del profesorado universitario en TIC. Aplicación del método Delphi para la selección de los contenidos formativos. Educación XX1, 17(1), 111-132. https://doi.org/10.5944/educxx1.17.1.10707
Cabero, J., & Barroso, J. (2013). La utilización del juicio de experto para la evaluación de TIC: el coeficiente de competencia experta. Bordón. Revista de Pedagogía, 65(2), 25-38. https://doi.org/10.13042/brp.2013.65202
Cabero, J., & Infante, A. (2014). Empleo del método Delphi y su empleo en la investigación en comunicación y educación. EDUTEC. Revista electrónica de tecnología educativa, 48, a272-a272. https://doi.org/10.21556/edutec.2014.48.187
Cabero, J., & Llorente, M. C. (2013). La aplicación del juicio de experto como técnica de evaluación de las tecnologías de la información y comunicación (TIC). Revista de Tecnología de Información y Comunicación en Educación, 7(2), 11-22.
Charalambous, C.Y., & Praetorius, A.K. (2018). Studying mathematics instruction through different lenses: setting the ground for understanding instructional quality more comprehensively. ZDM Mathematics Education, 50(3), 355–366. https://doi.org/10.1007/s11858-018-0914-8
Clayton, M. J. (1997). Delphi: a technique to harness expert opinion for critical decision‐making tasks in education. Educational psychology, 17(4), 373-386. https://doi.org/10.1080/0144341970170401
Diego-Mantecón, J. M., & Córdoba-Gómez, F. J. (2019). Adaptación y validación del MRBQ (Mathematics-Related Beliefs Questionnaire) al contexto colombiano con estudiantes de secundaria. Educación matemática, 31(1), 66-91. https://doi.org/10.24844/em3101.03
Dolores, C., & Ibáñez, G. (2020). Conceptualizaciones de la Pendiente en Libros de Texto de Matemáticas. Bolema: Boletim de Educação Matemática, 34, 825-846. https://doi.org/10.1590/1980-4415v34n67a22
Duval, R. (1993). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En E. Hitt (Ed.), Investigaciones en Matemática Educativa II (pp. 173-201). Grupo Editorial Iberoamérica.
Eccius-Wellmann, C., Lara-Barragán, A. G., Martschink, B., & Freitag, S. (2017). Comparación de perfiles de ansiedad matemática entre estudiantes mexicanos y estudiantes alemanes. Revista iberoamericana de educación superior, 8(23), 69-83. https://doi.org/10.22201/iisue.20072872e.2017.23.246
Garzón, D. (2017). Análisis de las decisiones del profesor de matemáticas en su gestión de aula. Revista Educación Matemática, 29(3), 131-160. https://doi.org/10.24844/EM2903.05
Gordon, T. J. (1994). The Delphi method. In J.C. Glenn & T.J. Gordon (Eds.). Futures Research Methodology Version 2.0. (CD-Rom). American Council for the United Nations University.
Hill, H., Blunk, M.L., Charalambous, C.Y., Lewis, J.M., Phelps, G.C., Sleep, L., & Ball, D. (2008). Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study. Routledge Cognition and Instruction, 26(4). https://doi.org/10.1080/07370000802177235
Kaiser, G. (2020) Mathematical Modelling and Applications in Education. In S. Lerman (Eds.), Encyclopedia of Mathematics Education. Springer. https://doi.org/10.1007/978-3-030-15789-0_101
Landeta, J. (1999). El método Delphi. Una técnica de previsión para la incertidumbre. Ariel.
Linstone, H. A., & Turoff, M. (1975). The delphi method. Addison-Wesley.
Liu, R. D., Wang, J., Star, J. R., Zhen, R., Jiang, R. H., & Fu, X. C. (2018). Turning potential flexibility into flexible performance: Moderating effect of self-efficacy and use of flexible cognition. Frontiers in psychology, 9, 646. https://doi.org/10.3389/fpsyg.2018.00646
Llorente, L. (2013). Assessing Personal Learning Environments (PLEs). An expert evaluation. Journal of New Approaches in Educational Research), 2(1), 39-44. https://doi.org/10.7821/naer.2.1.39-44
López-Gómez, E. (2018). El método Delphi en la investigación actual en educación: una revisión teórica y metodológica. Educación XX1, 21(1), 17-40. https://doi.org/10.5944/educXX1.20169
Ludwig, B. (1997). Predicting the future: Have you considered using the Delphi methodology. Journal of extension, 35(5), 1-4.
Martínez, A. (1988). Diseños experimentales: métodos y elementos de teoría. Trillas.
Martino, J. (1999). Thirty years of change and stability. Technological Forecasting and Social Change, 62(1-2), 13-18. https://doi.org/10.1016/S0040-1625(99)00011-6
Martins, G. A., & Theóphilo, C. R. (2007). Metodologia da Investigação Científica para Ciências Sociais Aplicadas. Atlas
Matsumura, L. C., Garnier, H., Slater, S. C., & Boston, M. (2008). Toward measuring instructional interactions ‘at-scale’. Educational Assessment, 13(4), 267–300. https://doi.org/10.1080/10627190802602541
Maz-Machado, A., Madrid, M. J., León-Mantero, C., & Jiménez-Fanjul, N. (2019). Mathematical practical sessions with manipulatives: Trainee teachers’ perceptions of their utility. South African Journal of Education, 39(2), Art. #1620. https://doi.org/10.15700/saje.v39ns2a1620
McMillan, S.S., King, M., & Tully, M.P. (2016). How to use the nominal group and Delphi techniques. International Journal of Clinic Pharmacy, 38, 655–662. https://doi.org/10.1007/s11096-016-0257-x
Mengual, S., Roig, R., & Mira, J.B. (2016). Delphi study for the design and validation of a questionnaire about digital competences in higher education. International Journal of Educational Technology in High Education, 13, 12. https://doi.org/10.1186/s41239-016-0009-y
Molina, O., & Samper, C. (2019). Tipos de problemas que provocan la generación de argumentos inductivos, abductivos y deductivos. Bolema: Boletim de Educação Matemática, 33, 109-134. https://doi.org/10.1590/1980-4415v33n63a06
Moore, C. M. (1987). Group techniques for idea building. Sage Publications, Inc.
Novakowski, N., & Wellar, B. (2008). Using the Delphi technique in normative planning research: methodological design considerations. Environment and Planning A, 40(6), 1485-1500. https://doi.org/10.1068/a39267
Okoli, C., & Pawlowski, S. D. (2004). The Delphi method as a research tool: an example, design considerations and applications. Information & management, 42(1), 15-29. https://doi.org/10.1016/j.im.2003.11.002
Openshaw, R., & Walshaw, M. (2019). Transnational Synergies in School Mathematics and Science Debates. Springer Nature. https://doi.org/10.1007/978-3-030-28269-1
Orton, A. (2003). Didáctica de las matemáticas. Ministerio de Educación, Cultura y Deporte-Ediciones Morata.
Parenté, F. J., & Anderson, J.K. (1987). Delphi inquiry systems. En G. Wright & P. Ayton (Eds.), Judgemental Forecasting (pp. 129-156). John Wiley.
Patton, M. (1990). Qualitative evaluation and research methods. Newbury Park, CA.
Piburn, M., & Sawada, D. (2000). Reformed teaching observation protocol (RTOP): Reference manual. Technical Report. Arizona Collaborative for Excellence in the Preparation of Teachers.
Planas, N., Arnal-Bailera, A., & García-Honrado, I. (2018). El discurso matemático del profesor: ¿Cómo se produce en clase y cómo se puede investigar? Enseñanza de las Ciencias, 36(1), 45-60. https://doi.org/10.5565/rev/ensciencias.2240
Praetorius, A. K., & Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: looking back and looking forward. ZDM Mathematics Education, 50(3), 535-553. https://doi.org/10.1007/s11858-018-0946-0
Rodríguez, J.M., & Ruiz, J. (2019). El clima social en centros educativos: percepción del profesorado de Educación Secundaria Obligatoria de la Comunidad de Madrid. Revista de Investigación Educativa, 37(1), 231-250. https://doi.org/10.6018/rie.37.1.320541
Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Transformation: Using examples in mathematics teaching. In Developing Primary Mathematics Teaching: Reflecting on Practice with the Knowledge Quartet (pp. 67-100). SAGE Publications. https://doi.org/10.4135/9781446279571
Schlesinger, L., & Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Mathematics Education, 48, 29–40. https://doi.org/10.1007/s11858-016-0765-0
Schneider, M., Rittle-Johnson, B., & Star, J. R. (2011). Relations between conceptual knowledge, procedural knowledge, and procedural flexibility in two samples differing in prior knowledge. Developmental Psychology, 47(6), 1525-1538. https://doi.org/10.1037/a0024997
Shah, H., & Kalaian, S. A. (2009). Which Parametric Statistical Method to Use For Analyzing Delphi Data? Journal of Modern Applied Statistical Method, 8(1), 226-232. https://doi.org/10.22237/jmasm/1241137140
Teddlie, C., Creemers, B., Kyriakides, L., Muijs, D., & Yu, F. (2006). The international system for teacher observation and feedback: Evolution of an international study of teacher effectiveness constructs. Educational Research and Evaluation, 12(6), 561–582. https://doi.org/10.1080/13803610600874067
Thomas, C. A., & Berry III, R. Q. (2019). A Qualitative Metasynthesis of Culturally Relevant Pedagogy & Culturally Responsive Teaching: Unpacking Mathematics Teaching Practices. Journal of Mathematics Education at Teachers College, 10(1), 21-30. https://doi.org/10.7916/jmetc.v10i1.1668
Thompson, C. J., & Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: Improving design and rigour. Mathematics Education Research Journal, 26(2), 301–323. https://doi.org/10.1007/s13394-013-0099-y
van den Ham, A. K., & Heinze, A. (2018). Does the textbook matter? Longitudinal effects of textbook choice on primary school students’ achievement in mathematics. Studies in Educational Evaluation, 59, 133-140. https://doi.org/10.1016/j.stueduc.2018.07.005
Van Zoest, L. R., Peterson, B. E., Rougée, A. O., Stockero, S. L., Leatham, K. R., & Freeburn, B. (2021). Conceptualizing important facets of teacher responses to student mathematical thinking. International Journal of Mathematical Education in Science and Technology, 1-26. https://doi.org/10.1080/0020739X.2021.1895341
Vergnaud, G. (2013). Pourquoi la théorie des champs conceptuels? Infancia y Aprendizaje, 36(2), 131-161. https://doi.org/10.1174/021037013806196283
von der Gracht, H.A. (2012). Consensus measurement in Delphi studies: review and implications for future quality assurance. Technological Forecasting and Social Change, 79(8), 1525-1536. https://doi.org/10.1016/j.techfore.2012.04.013
Walkowiak, T. A., Berry, R. Q., Meyer, J. P., Rimm-Kaufman, S. E., & Ottmar, E. R. (2014). Introducing an observational measure of standards-based mathematics teaching practices: Evidence of validity and score reliability. Educational Studies in Mathematics, 85(1), 109–128. https://doi.org/10.1007/s10649-013-9499-x
Weber, K. E., Gold, B., Prilop, C. N., & Kleinknecht, M. (2018). Promoting pre-service teachers' professional vision of classroom management during practical school training: Effects of a structured online-and video-based self-reflection and feedback intervention. Teaching and Teacher Education, 76, 39-49. https://doi.org/10.1016/j.tate.2018.08.008
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2021 RELIEVE - Revista Electrónica de Investigación y Evaluación Educativa

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Los autores ceden de forma no exclusiva los derechos de explotación de los trabajos publicados a RELIEVE (a los solos efectos de favorecer la difusión de los artículos publicados:firmar contratos de difusión, de integración en bases de datos, etc.) y consienten que se distribuyan bajo la licencia de Creative Commons Reconocimiento-Uso No Comercial 4.0 International (CC-BY-NC 4.0), que permite a terceros el uso de lo publicado siempre que se mencione la autoría de la obra y la fuente de publicación, y se haga uso sin fines comerciales.
Los autores pueden llegar a otros acuerdos contractuales adicionales e independientes, para la distribución no exclusiva de la versión del trabajo publicado en esta revista (por ejemplo, incluyéndolo en un repositorio institucional o publicándolo en un libro), siempre y cuando se cite claramente que la fuente original de publicación es esta revista.
La mera remisión del artículo a RELIEVE supone la aceptación de estas condiciones.













