Artículos
Inferencia causal en investigación educativa: Análisis de la causalidad en estudios observacionales de carácter transversal
Causal inference in educational research: Causal analysis in cross-sectional observational studies
Inferência causal em investigação educativa: Análise da causalidade em estudos observacionais de caráter transversal
教育研究中的因果推断:对观察性横断面研究的因果关系进行分析
الاستدلال السببي في البحوث التربوية: تحليل السببية في الدراسات الرصدية المستعرضة
Inferencia causal en investigación educativa: Análisis de la causalidad en estudios observacionales de carácter transversal
RELIEVE. Revista Electrónica de Investigación y Evaluación Educativa, vol. 29, núm. 2, 2023
Universidad de Granada

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Recepción: 13 Diciembre 2022
Aprobación: 12 Julio 2023
Publicación: 11 Diciembre 2023
Financiamiento
Fuente: MCIN/AEI/10.13039/501100011033/ y por FEDER Una manera de hacer Europa.
Beneficiario: Proyecto PID2021-125775NB-I00
Resumen: La suposición de relaciones causa-efecto en la investigación ex post facto es un problema ampliamente conocido en el ámbito de la metodología de investigación en ciencias sociales. Para abordar esta importante limitación, en los últimos años se ha extendido el empleo de técnicas de inferencia causal, un conjunto de procedimientos estadísticos establecidos para poder extraer conclusiones causales en investigaciones no experimentales. A pesar de su amplia popularidad y difusión en el ámbito de las ciencias sociales y de la salud, su uso en investigación educativa es todavía marginal. Así, este trabajo introduce las principales técnicas de inferencia causal disponibles para el investigador educativo cuando dispone de datos observacionales de panel. Tras abordar las características clave y el potencial de las técnicas de emparejamiento por puntuación de propensión, variables instrumentales y diseño de regresión discontinua, se presenta un ejemplo de aplicación de cada una de ellas empleando las bases de datos obtenidas en la evaluación PISA 2018. Se incluye la competencia matemática como variable dependiente en todos los modelos propuestos. Dada las diferentes características de cada una de estas técnicas, la variable independiente empleada varía en los tres modelos aplicados: asistencia a educación infantil en el emparejamiento por puntuación de propensión, expectativas académicas del estudiante en variables instrumentales y tamaño del municipio en el que se encuentra la escuela en diseño de regresión discontinua. Se concluye el artículo discutiendo el potencial de este conjunto de técnicas, teniendo en cuenta las necesidades y procedimientos metodológicos más habitualmente aplicados en la investigación educativa.
Palabras clave: Análisis causal, metodología estadística, evaluación, análisis de datos.
Abstract: The assumption of cause-effect relationships in ex post facto research is a widely known issue in the field of research methods in social sciences. To address this important limitation, the use of causal inference techniques has become widespread in recent years. Causal inference establishes a set of statistical procedures for drawing causal conclusions in non-experimental research. Despite its wide popularity and diffusion in the social and health sciences, its use in educational research is still marginal. Thus, this paper introduces the main causal inference techniques available to the educational researcher when observational panel data are available. After addressing the key features and potential of propensity score matching, instrumental variables, and regression discontinuity design, we present an example application of each of these techniques. We used the available databases from the PISA 2018 assessments. We included the mathematical competence as the dependent variable in all the three models implemented. Given the different characteristics of each of these techniques, the independent variable used is different in the three models applied: attendance to early childhood education in propensity score matching; student academic expectations in instrumental variables; and size of the community in which the school is located in regression discontinuity design. The article concludes by discussing the potential of this set of techniques, taking into account the needs and methodological procedures most commonly applied in educational research.
Keywords: causal analysis, statistical methods, evaluation, data analysis.
Resumo: A assunção de relações de causa-efeito na investigação ex post facto é um problema amplamente conhecido no domínio da metodologia de investigação em ciências sociais. Para fazer face a esta importante limitação, a utilização de técnicas de inferência causal, um conjunto de procedimentos estatísticos estabelecidos para poder tirar conclusões causais em investigações não experimentais, tem vindo a generalizar-se nos últimos anos. Apesar da sua grande popularidade e disseminação no âmbito das ciências sociais e da saúde, a sua utilização em investigação educativa é ainda marginal. Assim, este documento introduz as principais técnicas de inferência causal disponíveis para o investigador educativo quando existem dados observacionais de painel. Depois de discutir as principais características e o potencial das técnicas de correspondência por pontuação de propensão, variáveis instrumentais e conceção de regressão descontínua, apresenta-se um exemplo da aplicação de cada uma delas utilizando as bases de dados obtidas na avaliação PISA 2018. A competência matemática é incluída como variável dependente em todos os modelos propostos. Dadas as diferentes características de cada uma destas técnicas, a variável independente utilizada varia nos três modelos aplicados: assistência ao ensino infantil na correspondência por pontuação de propensão, expectativas académicas do estudante em variáveis instrumentais e dimensão do município em que a escola se localiza em conceção de regressão descontínua. O artigo conclui discutindo o potencial deste conjunto de técnicas, tendo em conta as necessidades e os procedimentos metodológicos mais comummente aplicados na investigação educativa.
Palavras-chave: Análise causal, metodologia estatística, avaliação, análise de dados.
摘要: 事后回溯研究中的因果关系假设是社会科学研究方法领域普遍公认的问题。为了了解这一局限性,最近几年开始广泛地使用因果推断技术。这项技术是指通过一系列已建立的统计学过程从非实验研究中提取因果结论的技术。虽然该技术在社会科学和健康科学领域有着广泛的认知度和使用度,但在教育领域它还处在边缘位置。因此,该研究导入可用的主要因果推断技术,帮助教育研究者分析观察性面板数据。研究首先详述了倾向性得分匹配、工具变量、断点回归设计的主要特点和潜力,然后分别展示了这些技术在2018年国际学生评估项目(PISA2018)测试数据上的应用示例。在所有的建议模型中,数学能力都作为因变量出现。考虑到每项技术的特殊性,三种模型使用不同的自变量:在倾向性得分匹配模型中的幼儿教育出勤率;在工具变量模型中的学生学业期待以及断点回归设计中学校所在的城区规模。在考虑到教学研究需求和常规方法论应用过程的基础上,该研究还对一系列技术的潜力进行了讨论。
關鍵詞: 技能, 教师培养, 学生, 学习计划.
ملخص: يعد افتراض العلاقات بين السبب والنتيجة في الأبحاث بأثر رجعي مشكلة معروفة على نطاق واسع في مجال منهجية البحث في العلوم الاجتماعية. ولمعالجة هذا القيد المهم, انتشر في السنوات الأخيرة استخدام تقنيات الاستدلال السببي, وهي مجموعة من الإجراءات الإحصائية التي تم وضعها لتكون قادرة على استخلاص استنتاجات سببية في البحوث غير التجريبية. وعلى الرغم من شعبيتها وانتشارها الواسع في مجال العلوم الاجتماعية والصحية, إلا أن استخدامها في البحوث التربوية لا يزال هامشيًا. وبالتالي, يقدم هذا العمل تقنيات الاستدلال السببي الرئيسية المتاحة للباحث التربوي عند توفر بيانات لوحة المراقبة. بعد معالجة الخصائص الرئيسية وإمكانات مطابقة درجات الميل, والمتغيرات الآلية, وتقنيات تصميم الانحدار المتقطع, يتم تقديم مثال لتطبيق كل منها باستخدام قواعد البيانات التي تم الحصول عليها في تقييم PISA2018.تم تضمين الكفاءة الرياضية كمتغير تابع في جميع النماذج المقترحة.وبالنظر إلى الخصائص المختلفة لكل من هذه التقنيات, فإن المتغير المستقل المستخدم يختلف في النماذج الثلاثة المطبقة: الحضور في التعليم في مرحلة الطفولة المبكرة في مطابقة درجات الميل, والتوقعات الأكاديمية للطلاب في المتغيرات المفيدة والحجمللبلدية التي تقع فيها المدرسة في تصميم تراجعي متقطع.ويختتم المقال بمناقشة إمكانات هذه المجموعة من التقنيات, مع الأخذ في الاعتبار الاحتياجات والإجراءات المنهجية الأكثر شيوعًا في البحث التربوي
الكلمات المفتاحية: التحليل السببي, المنهجية الإحصائية, التقييم, تحليل البيانات.
Introducción
Inferencia causal en la investigación no experimental
Los diseños experimentales se emplean para la verificación de hipótesis de investigación y, con ello, la atribución de relaciones causales entre dos o más variables. Aunque en ciencias sociales se conceptualizan algunos diseños que permitirían atribuir causalidad en ambientes menos controlados (Campbell & Stanley, 1963), la investigación experimental busca fundamentalmente un control estricto del diseño de la investigación: asignación aleatoria de grupos, manipulación total de la variable independiente, medida objetiva de la variable dependiente, y máximo control de los sesgos asociados a las variables extrañas o covariables identificadas. No obstante, en numerosas ocasiones no es factible llevar a cabo diseños estrictamente experimentales en la investigación socioeducativa por diversas razones de carácter operativo, ético o económico, entre otras.
Cuando no es posible la aleatorización y el control exhaustivo de variables, lo más habitual es el desarrollo de estudios observacionales, también conocidos como no experimentales o de carácter ex post facto. En la literatura se identifica la limitación fundamental de este tipo de diseños en su carácter ex post facto (Altman, 2020; Kerlinger & Lee, 1999): dado que en estos estudios los grupos vienen predeterminados por las condiciones previas de la muestra, existen sesgos en su comparación derivados de las diferentes características de los sujetos de cada grupo.
En los últimos años se ha popularizado el empleo de técnicas estadísticas de inferencia causal, que buscan superar el alcance correlacional asociado a los diseños no experimentales, proponiendo diferentes procedimientos para controlar este sesgo de comparación (Antonakis et al., 2010; Imai et al., 2011; Imbens & Rubin, 2015; Pearl & Mackenzie, 2018). En concreto, las técnicas más extendidas en la investigación social para realizar inferencias causales con datos observacionales de carácter transversal son las siguientes:
· Propensity Score Matching (PSM)
· Variables Instrumentales (IV)
· Diseño de Regresión Discontinua (RDD)
Dado que estas técnicas se han desarrollado a partir de enfoques claramente diferenciados, resulta importante seleccionar la más apropiada en función de las necesidades de la investigación, la naturaleza de las variables disponibles en la misma y el modelo causal que desee validarse. Así, teniendo en cuenta su carácter emergente y su potencial en la investigación educativa, este trabajo pretende analizar las características y posibilidades que ofrecen las técnicas PSM, IV y RDD (por sus siglas en inglés) para realizar inferencias causales. Para ello, tras realizar una revisión conceptual de las tres técnicas, se ejemplificará su uso a través de tres modelos propuestos a partir de los datos de la muestra española de estudiantes y centros educativos en PISA 2018.
Difusión de la inferencia causal en la investigación educativa
La aplicación de técnicas de inferencia causal en la investigación educativa es a día de hoy limitada, con bajos niveles de difusión en comparación con otros ámbitos afines dentro de las ciencias sociales y de la salud (figura 1).
De hecho, la evolución de la publicación de trabajos de inferencia causal en las revistas del ámbito educativo mantiene unas cifras muy discretas durante este primer cuarto de siglo (figura 2), con una tendencia incluso decreciente en los últimos años. Y los trabajos que emplean muestras españolas en evaluaciones a gran escala son contados: la mayor parte aplican variables instrumentales (Castro Aristizabal et al., 2017; Choi et al., 2012; Cordero & Gil-Izquierdo, 2018; Lopez-Agudo et al., 2021) y se emplea propensity score matching marginalmente (Crespo-Cebada et al., 2014; García-Pérez & Hidalgo-Hidalgo, 2017), no encontrándose trabajos que implementen diseños de regresión discontinua.
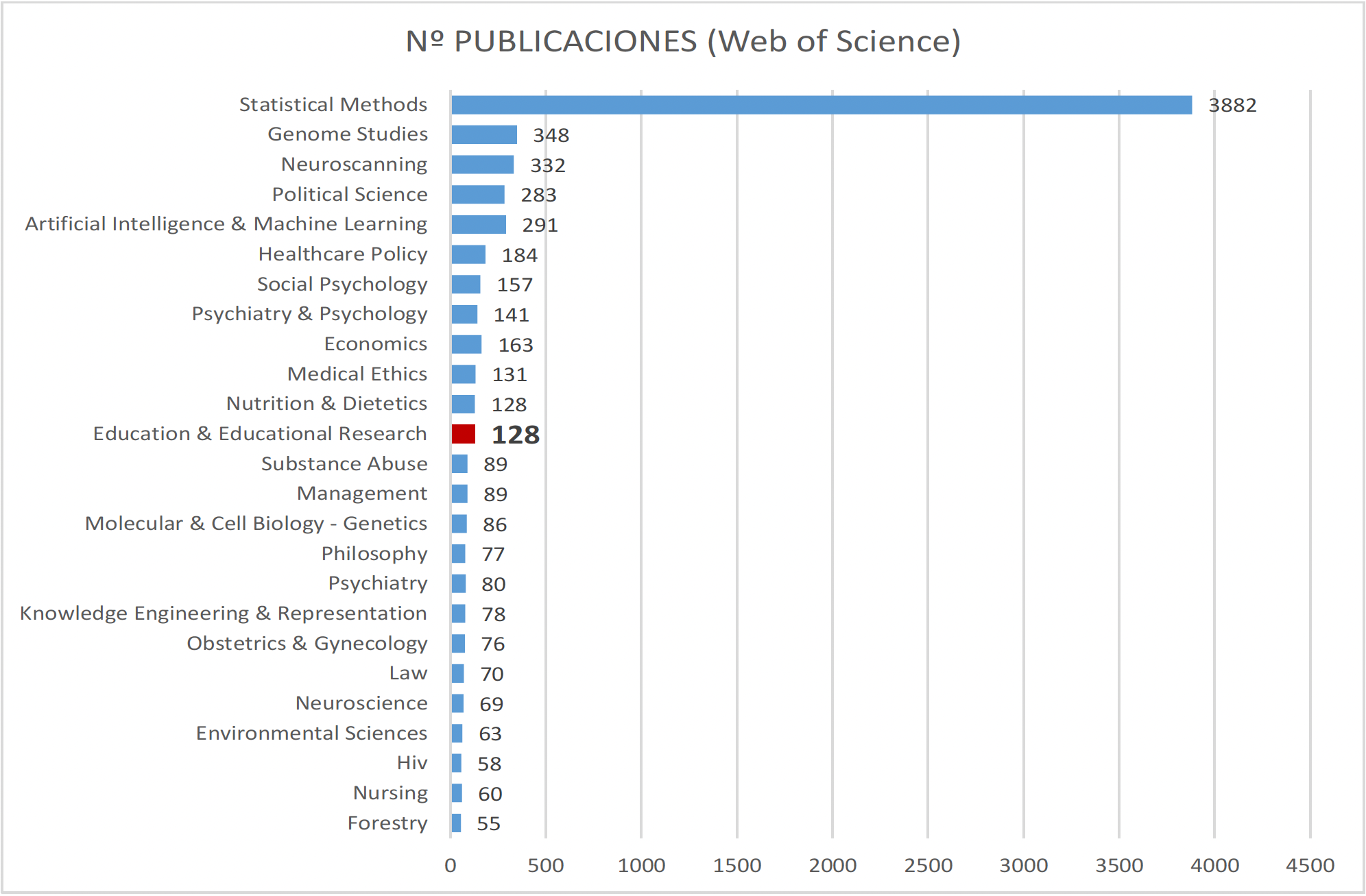
Figura 1.
Áreas con más de 50 publicaciones sobre “causal inference” (Web of Science, 6/12/2022)
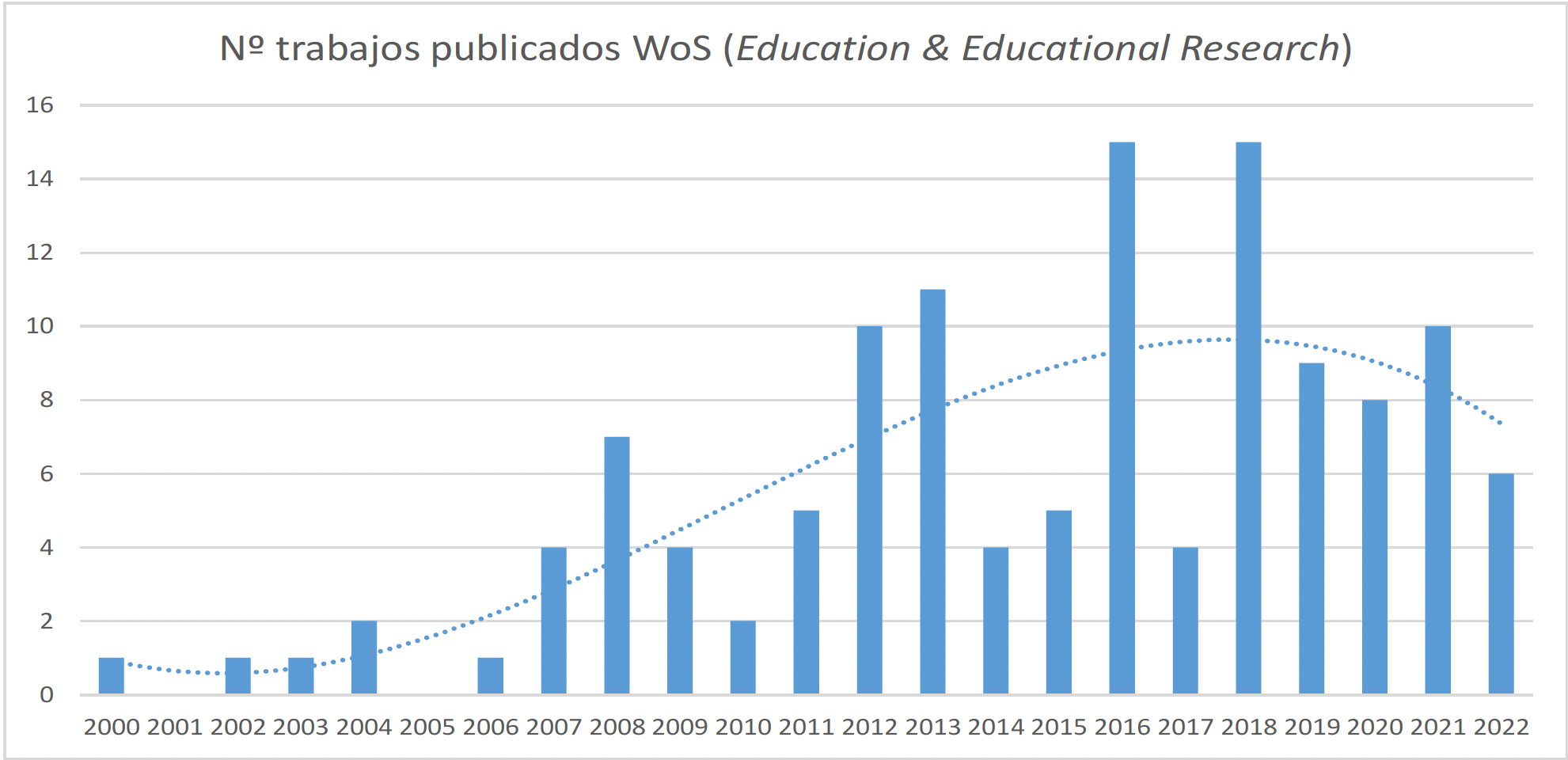
Figura 2.
Publicaciones sobre “causal inference” en área ‘Education & Educational Research’ (Web of Science, 6/12/2022)
Propensity Score Matching: agrupación de pares ‘gemelos’
Los diseños orientados a estimar efectos causales de un tratamiento en relación a un control, considerando tratamiento . control como dos niveles diferentes de la variable independiente, se enfocan en el conjunto de actividades del tratamiento que preceden al rasgo medido en la variable dependiente o resultado (Rosenbaum & Rubin, 2022). Dado que no podemos observar los resultados de los individuos tanto bajo tratamiento como bajo control, estos diseños se aplican bajo la asunción de que, si no se desarrollaran el conjunto de actividades del tratamiento, la variable dependiente se mantendría estable. Podemos definir esta lógica como razonamiento contrafáctico (Rubin, 1974). Un problema fundamental es que este efecto potencial en la variable dependiente si en lugar de aplicar al grupo el nivel tratamientose le hubiera aplicado el nivel control no es directamente observable. Por eso para garantizar la adecuada estimación de los efectos causales en la investigación experimental se incluye el grupo control, buscando la homogeneidad máxima entre grupo experimental y grupo control (Kaplan, 2016). Así, ambos grupos deben tener distribuciones similares en el conjunto de covariables que podrían afectar a la relación causal planteada, y si no es posible controlar alguna de estas variables se confía en la distribución aleatoria de los sujetos a las condiciones control y experimental.
Sin embargo, existen condicionantes prácticos y éticos en la investigación en ciencias sociales que dificultan, o incluso imposibilitan, la definición de las condiciones tratamiento y control en el trabajo de campo. Estas investigaciones se ven obligadas a implementar estudios observacionales con diseños no experimentales o, en el mejor de los casos, diseños pre-experimentales.
Bajo esta lógica surge la técnica PSM, que propone el emparejamiento de sujetos de dos grupos diferentes a partir de su homogeneidad en cuanto a un conjunto de covariables establecido. Teóricamente, los dos grupos establecen la condición control y experimental (por ejemplo: haber repetido curso o no haberlo hecho, estudiar en una escuela privada o en una escuela pública, haber cursado o no educación infantil, etc.), y las covariables se entienden como las variables controladas en el experimento. Tras el emparejamiento, se puede considerar a las parejas de sujetos de los grupos control y experimental como ‘gemelos’, y conceptualmente es posible comprobar el efecto causal del tratamiento sobre la variable dependiente.
Este emparejamiento se realiza a partir del cálculo del PropensityScore (PS) de cada sujeto en ambos grupos, que se define en Rosenbaum y Rubin (1983) como la probabilidad condicional de asignación al tratamiento, dado un conjunto de covariables:
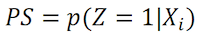
donde la variable Z se refiere a la pertenencia del sujeto al grupo experimental (Z=1) o control (Z=0), y Xi son el conjunto de covariables definidas.
Se asumen dos supuestos fundamentales en la aplicación del PSM (Rosenbaum & Rubin, 2022; Rutkowski & Delandshere, 2016):
1. Ignorabilidad: Todas las covariables clave que afectan a la relación causal estudiada están identificadas y controladas. La existencia de covariables clave no observadas puede suponer importantes sesgos en la comparabilidad de los grupos (Kaplan, 2016). Dado que no es posible testar directamente el cumplimiento de este supuesto, es esencial planificar cuidadosamente este tipo de investigaciones.
2. Superposición: Los valores del propensity score (probabilidad del sujeto de recibir el tratamiento) de cada emparejamiento están balanceados. El estadístico más aceptado para validar este supuesto es la diferencia media estandarizada (SMD, por sus siglas en inglés), que indica la diferencia de medias entre los dos grupos generados en el PSM (Ali et al., 2014).
Cumplidos estos supuestos, es posible estimar los efectos del tratamiento sobre la variable dependiente aplicando el contraste de hipótesis apropiado. Existe debate en la literatura sobre el empleo de técnicas inferenciales para grupos independientes o para grupos relacionados (Austin, 2011), dependiendo esta decisión del juicio de investigador.
Variables Instrumentales: control de la endogeneidad de las variables independientes
Mientras que PSM está indicado cuando disponemos de una variable dicotómica que establece una situación experimental y una situación control, la técnica IV se ha desarrollado pensando en la atribución de causalidad en modelos de regresión de una o más variables independientes (X) sobre una variable dependiente (Y). A pesar de que la regresión suele realizarse con datos observacionales de panel, y es por tanto de carácter correlacional, en muchos casos se asume como un modelo causal que lleva a la asunción de inferencias causales incorrectas. Esto se debe al problema de la endogeneidad de las variables independientes, que se produce cuando X tiene una correlación significativa con la diferencia entre la puntuación real y la puntuación pronosticada mediante la recta de regresión (error de Y), lo cual conduce a estimaciones sesgadas de los parámetros del modelo. El sesgo de endogeneidad se da fundamentalmente por 5 causas (Maydeu-Olivares et al., 2020; Wooldridge, 2010):
1. Variable omitida. Se omiten en el modelo variables relacionadas tanto con X como con Y.
2y. Error en la medición de X. Debido a este sesgo se obtiene la variable observada X*, estimando el modelo X*→Y en lugar del deseado X→Y.
3. Causalidad inversa. El efecto causal tiene realmente la dirección Y→X.
4. Causalidad recíproca. Existen efectos causales mutuos, tanto X→Y como Y→X, pero la segunda ruta es omitida en el modelo empírico.
5. Selección. La selección de la muestra o del tratamiento no es aleatoria. Lo que afecta a la estimación X→Y.
En este sentido, el procedimiento IV busca controlar la endogeneidad a partir del empleo de variables exógenas Z (Cinelli et al., 2022). Así, como se muestra en la figura 3, se establecen las condiciones bajo las cuales se puede considerar que un conjunto de variables Z establecen un control adecuado, inadecuado o engañoso de la relación causal entre un predictor X y un resultado Y, considerando la posible existencia de variables no observadas U (Cinelli et al., 2022; Huenermund et al., 2022). Los mismos autores también establecen ciertas condiciones bajo las que el control es innecesario. A nivel general, el modelo establecerá un control adecuado de la causalidad: (1) si Z es una variable causa tanto de X como de Y, sin que existan otras variables no observadas que son a su vez causa de Z e Y o de Z y X; y (2) si Z es una var¡”ble ’ausa de X pero no de Y, y existen variables U que son a la vez causa de Z e Y.
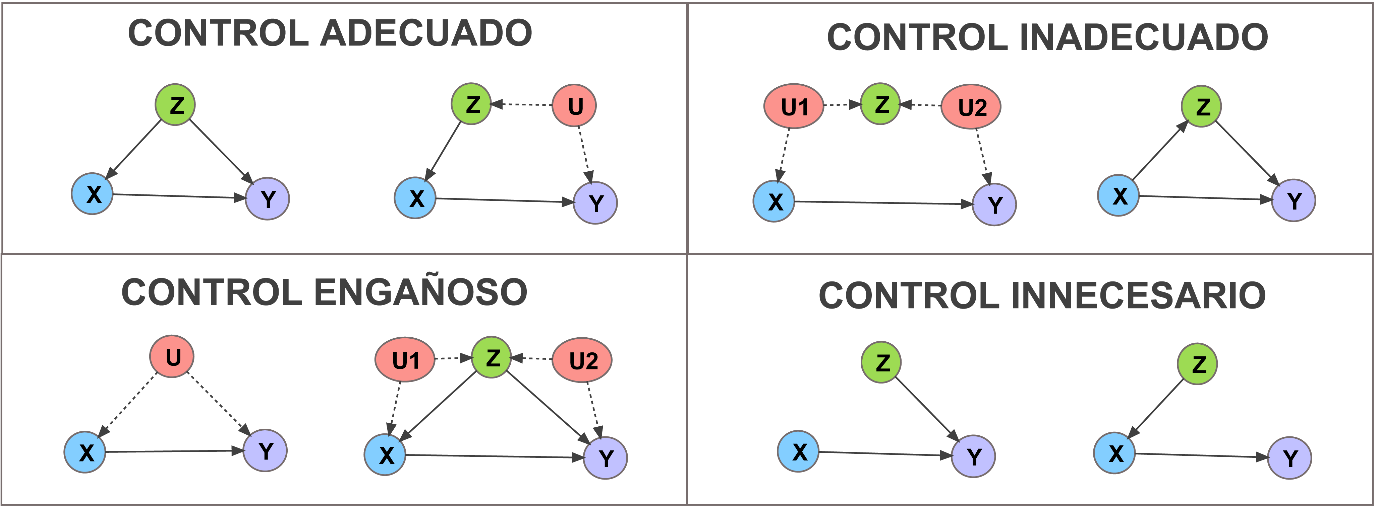
Figura 3.
Control de la endogeneidad a través de variables instrumentales
Estas variables Z son las denominadas variables instrumentales, que son variables exógenas al modelo de regresión X→Y con la función de seleccionar únicamente la variabilidad conjunta entre X y Z ( 2X|Z). De este modo, si se ha establecido un control adecuado es posible controlar la correlación entre X y los residuos de la variable dependiente. Por eso, la regresión IV se realiza en dos etapas (Angrist et al., 1996; Pokropek, 2016), y el método más habitual para su estimación es el de mínimos cuadrados en dos etapas (Maydeu-Olivares et al., 2020) o 2SLS, por sus siglas en inglés:
1. Realizar la regresión de X sobre las variables instrumentales Z:
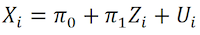
donde Ui se refiere al término de error de la regresión.
2. Regresión de Y sobre 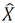 , que, gracias a la estimación previa, incluye la varianza común de X con Z:
, que, gracias a la estimación previa, incluye la varianza común de X con Z:

donde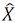 se refiere a la puntuación pronosticada en el primer paso y Ei es el término de error del modelo.
se refiere a la puntuación pronosticada en el primer paso y Ei es el término de error del modelo.
Además de probar un modelo con las condiciones adecuadas para que Z establezca un control adecuado, tal y como se expresa en la figura 2, se plantean otros supuestos fundamentales en la regresión IV:
· Endogeneidad (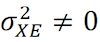 ): La estimación 2SLS tiene sentido, como alternativa a la estimación de Mínimos Cuadrados Ordinarios (MCO), cuando existe endogeneidad entre X y los residuos. Si X es exógena, ambos estimadores son consistentes, y MCO más eficiente, por lo que se recomienda emplear MCO.
): La estimación 2SLS tiene sentido, como alternativa a la estimación de Mínimos Cuadrados Ordinarios (MCO), cuando existe endogeneidad entre X y los residuos. Si X es exógena, ambos estimadores son consistentes, y MCO más eficiente, por lo que se recomienda emplear MCO.
· Relevancia (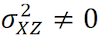 ): Los instrumentos y la variable independiente deben estar fuertemente correlacionados.
): Los instrumentos y la variable independiente deben estar fuertemente correlacionados.
· Exogeneidad ( ): Los instrumentos no pueden estar correlacionados con la variable Y, esto es, no puede existir correlación entre éstos y el error. Se puede testar la exogeneidad aplicando un contraste de sobreidentificación como el de Sargan (Jin, 2022), aunque para ello deben existir más variables instrumentales (VI) que variables independentes (X).
): Los instrumentos no pueden estar correlacionados con la variable Y, esto es, no puede existir correlación entre éstos y el error. Se puede testar la exogeneidad aplicando un contraste de sobreidentificación como el de Sargan (Jin, 2022), aunque para ello deben existir más variables instrumentales (VI) que variables independentes (X).
La figura 4 presenta las diferencias conceptuales entre los modelos IV y MCO. Mientras que MCO estima el parámetro de interés (que teóricamente indica el efecto causal X→Y) con la varianza completa de X, IV estima a partir de la variabilidad de X condicionada al instrumento Z.
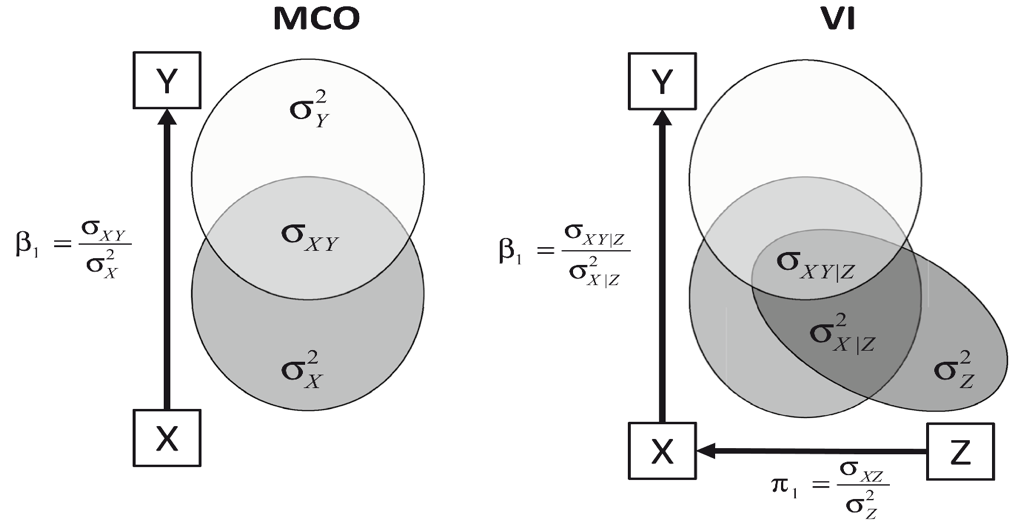
Figura 4.
Modelos conceptuales MCO e IV (Pokropek, 2016)
En conclusión, bajo el cumplimiento de las condiciones planteadas, en los modelos IV es posible considerar el parámetro 1 como el efecto causal que ejerce X sobre Y.
Diseño de Regresión Discontinua: control y experimento asignados en base a X
El RDD es aplicable cuando existe una variable observada X, de naturaleza continua, que determina la asignación de los sujetos a un tratamiento T, o al menos que influye sobre esta asignación. Bajo esta lógica, RDD busca estimar los efectos de un tratamiento separando a los participantes en dos grupos, tratamiento y control, atendiendo a un valor crítico de X (Ver Figura 4), que denominaremos k (Imbens & Lemieux, 2008; Lee & Lemieux, 2010). Es decir, se estimarán los efectos del tratamiento T a partir de una submuestra de sujetos similares en X, con puntuaciones alrededor de k. Así, además del valor k, será necesario estimar la amplitud del intervalo de puntuaciones alrededor de k incluidas en el análisis. A esta amplitud del intervalo la denominaremos h (Imbens & Kalyanaraman, 2012).
Así, RDD analiza el salto o discontinuidad existente en la distribución de la variable dependiente Y entre las puntuaciones X inmediatamente inferiores y superiores al punto k. El modelo RDD obtiene el efecto promedio de esta discontinuidad, o lo que es lo mismo, el efecto del tratamiento, estimando el peso de T en un modelo de regresión que incluye como variables independientes T, X y T*X. Este modelo se aplica únicamente en los sujetos con una puntuación X dentro del rango (k – h , k + h). La figura 5 muestra la interpretación visual de h y k en un diagrama de dispersión. El efecto causal del tratamiento (sujetos de color azul) sobre Y será estimado únicamente con los sujetos con puntuaciones Xi en el rango (-0.85 , 0.45), ya que el punto de corte es -0.2 y la amplitud del intervalo ±0.65.
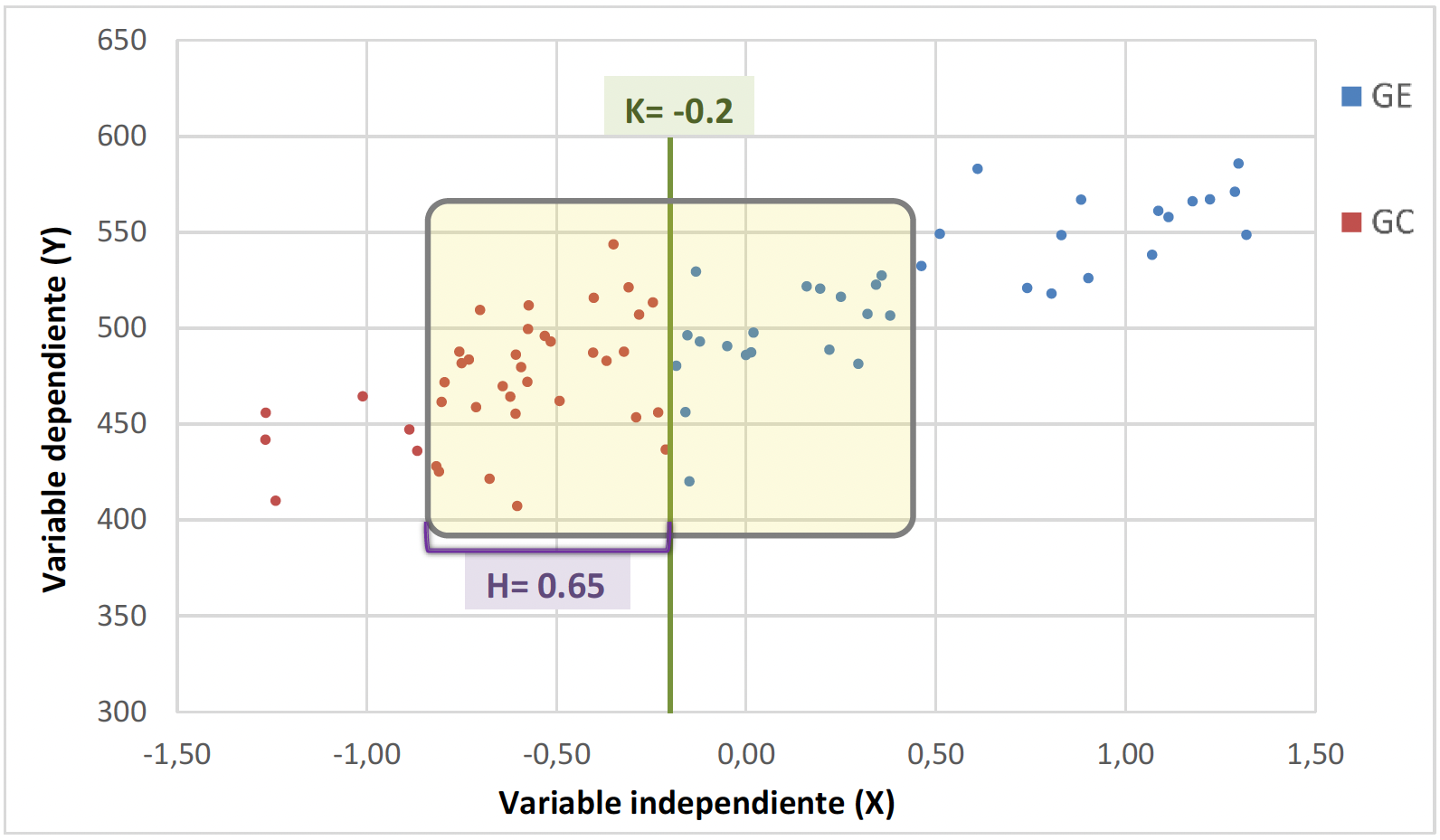
Figura 5.
Control de la endogeneidad a través de variables instrumentales
Por tanto, fijar los valores h y k es fundamental en RDD. Existen procedimientos estadísticos para estimar la amplitud óptima h, siendo la más popular la propuesta de Imbens y Kalyanaraman (2012). En relación a k, es establecida normalmente por el investigador bajo el supuesto fundamental de que la densidad de X alrededor de k es continua. Fijar el valor k es sencillo cuando, como en la figura 4, todos los sujetos no asignados al tratamiento están a su izquierda y todos los miembros asignados al tratamiento a su derecha. Este es el caso de la RDD nítida. No obstante, hay ocasiones en las que, a pesar de observarse una tendencia clara, existen sujetos asignados y no asignados al tratamiento tanto a la derecha como a izquierda de k. Es decir, hay veces en las que X no determina la asignación al tratamiento en todos los sujetos, sino que existe un error en la asignación Ti en algunos de ellos. Este es el caso de la RDD difusa.
El modelo lineal general de la RDD nítida es el siguiente[1]:
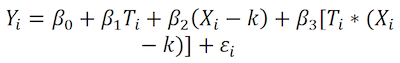
donde Yi es la variable dependiente, Ti una variable dummy con valores 1 y 0 para los sujetos que han recibido o no el tratamiento, (Xi-h) las puntuaciones de los sujetos en la variable continua que determina T, y i el término de error. Se puede observar que las puntuaciones Xi se centran en torno a k, de modo que los sujetos a la izquierda de k tendrán en el modelo puntuaciones negativas (Xi-k) y los sujetos a su derecha puntuaciones positivas (Xi-k). Así, el parámetro de interés del modelo para estimar el efecto causal del tratamiento es 1, considerado el efecto medio del tratamiento (ATE).
En el caso de la RDD difusa, dado que Ti no tiene una dependencia exacta de Xi, es necesario aplicar un procedimiento en dos pasos similar al IV. En el primer paso se estima la variable dependiente asignación o no asignación al tratamiento en función de (Xi-k):
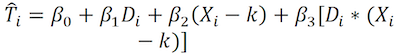
donde 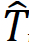 i es la estimación indicadora de si el sujeto es tratado o no, y Di una variable dummy con valores 0 y 1 para los sujetos que están respectivamente por debajo y por encima de k.
i es la estimación indicadora de si el sujeto es tratado o no, y Di una variable dummy con valores 0 y 1 para los sujetos que están respectivamente por debajo y por encima de k.
En el segundo paso se aplicará el modelo final para obtener el ATE:
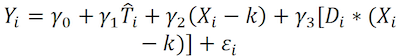
En este caso, el efecto del tratamiento ATE es el parámetro 1.
Método
Objetivo e hipótesis de la investigación
El objetivo de este trabajo es realizar una propuesta metodológica sobre la aplicación de técnicas de inferencia causal para el análisis de datos de panel en el marco de investigaciones ex post facto.
Así, los resultados presentan una breve ejemplificación de cada una de las tres técnicas propuestas a partir del análisis de datos secundarios procedentes de la evaluación PISA 2018 (OECD, 2019). Las hipótesis de investigación planteadas en cada uno de los modelos son las siguientes:
H1. La escolarización en educación infantil del estudiante ejerce un efecto causal positivo sobre su rendimiento académico durante la educación secundaria, independientemente de factores sociodemográficos y económicos clave (PSM).
H2. Las expectativas académicas futuras de los estudiantes de educación secundaria poseen efectos directos y significativos sobre su rendimiento académico, incluso controlando la endogeneidad con el nivel socioeconómico familiar (IV).
H3. El tamaño de la localidad en el que se encuentra la escuela (rural o urbana) no ejerce un efecto causal sobre el rendimiento de los estudiantes de educación secundaria (RDD), los efectos correlacionales encontrados se deben al nivel socioeconómico familiar.
Participantes
La población de referencia fue el conjunto de estudiantes españoles de educación secundaria de 15 años en el momento de la aplicación de PISA 2018. La muestra principal estuvo conformada por los n=35943 estudiantes y m=1089 escuelas españolas evaluadas.
Variables
La tabla 1 muestra las variables empleadas en cada uno de los modelos presentados. Por simplificar la interpretación de los resultados, se incluyó en todos los casos como variable dependiente la competencia o rendimiento en matemáticas. El nivel socioeconómico familiar (NSE) se incluyó como covariable en los 3 modelos. La selección de las variables independientes y covariables se realizó teniendo en cuenta el cumplimiento de los supuestos previos de cada modelo.
| PSM | IV | RDD | |
| Variable dependiente | Rendimiento en matemáticas (PV1MATH) | ||
| Variable independiente | Escolarización en Educación Infantil (DURECEC) | Expectativas académicas (ST225Q) | Tamaño del municipio (SC001Q01TA) |
| Covariables | Nivel socio-económico (ESCS) | ||
| Mes de nacimiento (ST003D02T) Estatus migratorio (IMMIG) Repetidor (REPEAT) Género (ST004D01T) | - | - | |
La covariable expectativa académica se recodificó a partir de las 6 variables facilitadas en PISA: Se estableció una puntuación para cada estudiante entre 1 y 6 puntos[2] en función de la expectativa de finalización de estudios más alta marcada por el estudiante (1=ESO; 2=FP Medio; 3=Bachiller; 5=FP Superior; 6=Universidad). La covariable Estatus migratorio fue recodificada en variable dicotómica: todos los estudiantes nacidos en España fueron considerados nativos (nativos e inmigrantes de segunda generación en PISA) y el resto inmigrantes. La covariable género incluye en PISA únicamente las categorías ‘hombre’ y ‘mujer’.
Procedimiento y análisis de datos
Con un nivel =5%, se aplicaron los siguientes procedimientos analíticos:
· Pesos muestrales: Dado que los modelos PSM y RDD seleccionan una submuestra a partir de la muestra inicial, se decidió no incluir los pesos muestrales como variable de ponderación.
· Valores perdidos: No se imputaron valores perdidos y se aplicó el procedimiento listwise deletion en los modelos. La proporción de valores perdidos en estas variables justifica esta decisión:
o Ningún valor perdido en rendimiento, mes de nacimiento y género
o Repetidor (1.4%), ESCS (1.8%), tamaño municipio (3.2%), estatus migratorio (3.1%), expectativas (4.3%), escolarización EI (14.7%)
· Valores plausibles: La OECD (2009) indica que, aunque el uso conjunto de los valores plausibles y las réplicas de los pesos muestrales es la alternativa más eficiente para la estimación de parámetros y errores típicos, el uso directo de uno de los valores plausibles permite estimaciones insesgadas de los parámetros. En coherencia con la decisión tomada en relación al uso de pesos muestrales, se decidió seleccionar un valor plausible. Así, en los tres modelos se empleó el primero de los valores plausibles del rendimiento en matemáticas.
En la aplicación de cada una de las técnicas se establece el siguiente procedimiento:
· PSM: Se emplea el SMD como estadístico de ajuste del balanceo o distancia entre los grupos tras aplicar el matching. Conforme a Zhang et al. (2019), se establece el valor SMD < .1 como indicador de buen balanceo. Se comprueba también la distancia de los cuadrados e interacciones entre covariables (Belitser et al., 2011). Tras comprobar el balanceo, se compara el rendimiento de ambos grupos mediante una prueba de t para grupos relacionados, incluyendo el tamaño del efecto (d de Cohen).
· IV: Se comprueba el supuesto de endogeneidad a través del test de Wu-Haussman (Hill et al., 2021), siendo la hipótesis alternativa (H0) que no existe endogeneidad. Para el supuesto de relevancia se aplica el contraste de instrumentos débiles (Maydeu-Olivares et al., 2020), siendo, en este caso, la hipótesis alternativa que el instrumento es débil. Se complementa el análisis de relevancia con el estadístico F (Stock & Yogo, 2005), estableciendo que los instrumentos son fuertes con F > 10. No se comprueba la exogeneidad dado que el modelo incluye una sola IV. Tras validar los supuestos previos, se compara el parámetro asociado a las expectativas académicas en los modelos MCO e IV.
· RDD: Se establece el valor h a partir del procedimiento Imbens-Kalyanaraman (2012), y se valida supuesto de continuidad de la variable X alrededor de k con el test de McCrary (2008), siendo la hipótesis alternativa que la variable es continua. Finalmente, se aplica RDD difusa para obtener el efecto medio del tratamiento T (escuela situada en entorno rural o urbano).
Resultados
PSM – Efecto causal de la escolarización en educación infantil sobre el rendimiento
Como se muestra en la figura 6, PISA incorpora la escolarización en EI en número de años. Atendiendo al análisis descriptivo e inferencial, se observa cómo la escolarización en EI tiene efectos significativos sobre el rendimiento, con una relación directa de efectos pequeños ( 2=0.018).
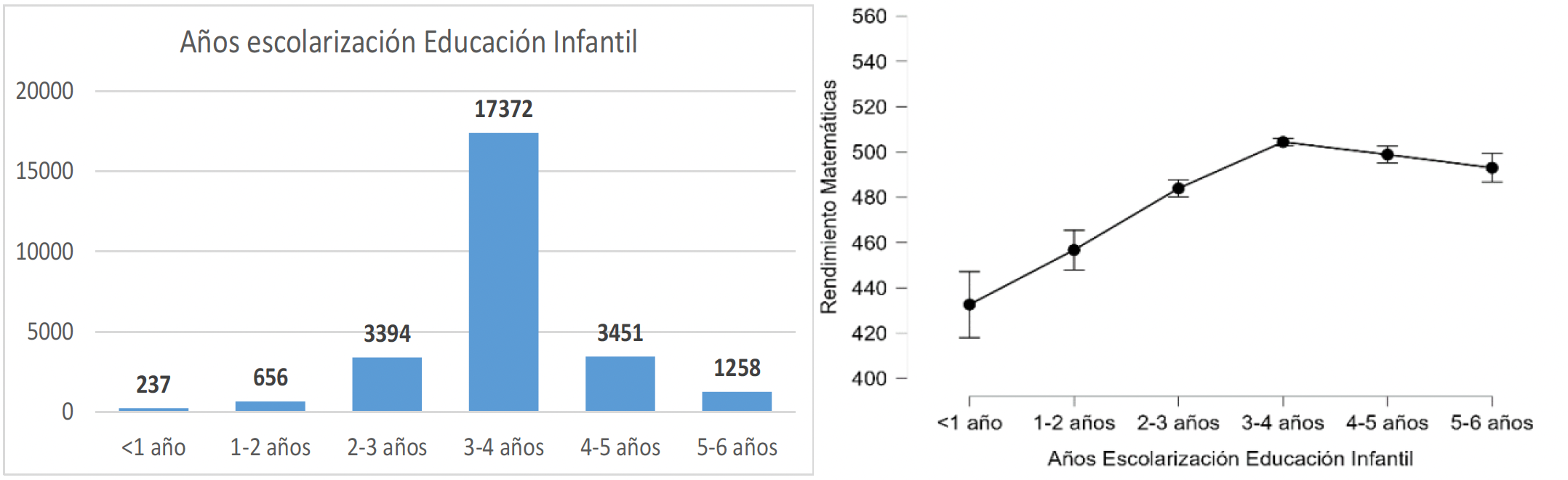
Figura 6.
Distribución de los años de escolarización en EI y relación con rendimiento
Se observa que el beneficio de los años de escolarización en EI se estabiliza a partir de los 2-3 años, por lo que el PSM dividirá a la muestra en 2 condiciones experimentales:
· Grupo control (GC): estudiantes con al menos 2 años de escolarización.
· Grupo del tratamiento o experimental (GE): estudiantes con menos de 2 años de escolarización.
La tabla 2 indica las diferencias entre GE y GC antes y después de aplicar el PSM. Mientras que en la muestra inicial aparecen diferencias significativas con tamaños del efecto moderados, tras el PSM ambos grupos resultan homogéneos en cuanto a las covariables. Tras la aplicación del PSM podemos afirmar que las muestras emparejadas se distribuyen aleatoriamente en los grupos control y del tratamiento. De hecho, mientras que el valor SMD de la distancia en la muestra inicial era de .563, en la muestra emparejada es de .001.
En la base de datos inicial los estudiantes del GE alcanzan niveles socioeconómicos claramente más bajos, duplican la tasa de repetición del otro grupo, muestran una mayor proporción de chicos sobre chicas, y presentan mayores tasas de estudiantes inmigrantes (observado tanto en el estatus migratorio como en el lenguaje en casa). El PSM, por tanto, ha realizado una selección de sujetos del GC de características similares a cada miembro del GE, descartando al resto de sujetos que no ofrecían un emparejamiento adecuado.
Cabe destacar antes de continuar que, debido a que el GE disponía de nGE = 893 sujetos, al realizar el emparejamiento la muestra seleccionada de estudiantes del GC es también de 893 sujetos, descartando el resto de sujetos de la muestra en este grupo (nGC = 25475). Este procedimiento es la clave del PSM, ya que se han seleccionado en el GC las parejas más similares o gemelas a sus pares del GE a partir de las covariables incorporadas. La figura 7 confirma que las distancias entre GE y GC en la muestra PSM son adecuadas tanto en las variables como en sus interacciones y cuadrados. Se han controlado los efectos espurios indeseables, y al considerar ambos grupos homogéneos se pueden estimar efectos causales.
| Prom. GC | Prom. GE | SMD | p. | r | ||
| NSEa | Inicial | -0.511 | 0.033 | -0.512 | <.001 | .295 |
| PSM | -0.511 | -0.536 | 0.023 | .794 | .010 | |
| Mes nacimientoa | Inicial | 6.642 | 6.551 | 0.026 | .429 | -.015 |
| PSM | 6.642 | 6.780 | -0.040 | .505 | -.027 | |
| Estatus migratoriob | Inicial | 29.68% | 5.18% | 0.536 | <.001 | .186 |
| PSM | 29.68% | 29.00% | 0.015 | .755 | .008 | |
| Repetidorb | Inicial | 44.01% | 20.80% | 0.468 | <.001 | .102 |
| PSM | 44.01% | 43.34% | 0.014 | .775 | .007 | |
| Génerob | Inicial | 42.22% | 52.69% | -0.212 | <.001 | -.038 |
| PSM | 42.22% | 40.54% | 0.034 | .471 | .017 | |
| Lenguaje casab | Inicial | 23.85% | 13.45% | 0.244 | <.001 | .055 |
| PSM | 23.85% | 24.41% | -0.013 | .782 | -.007 | |
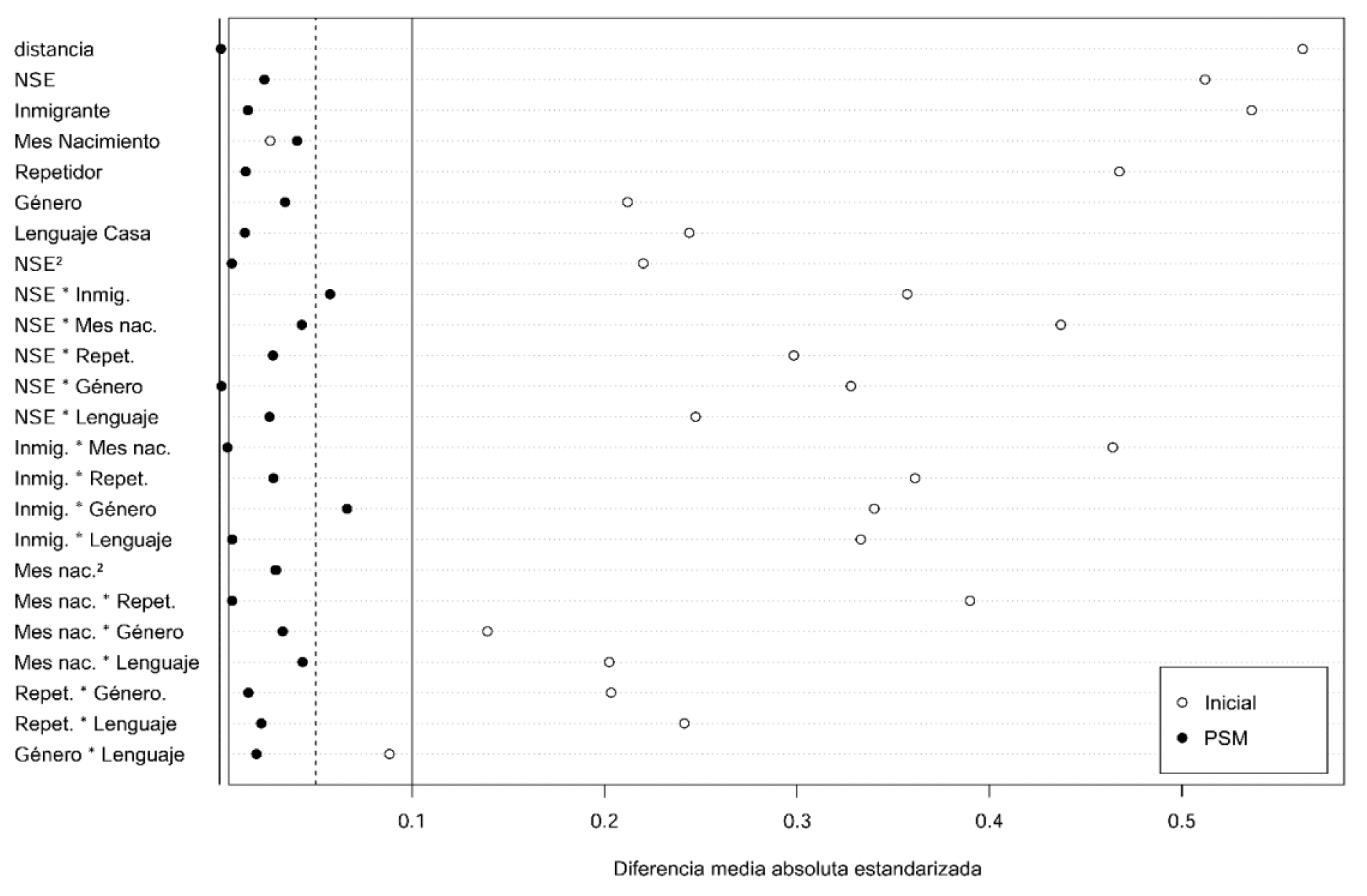
Figura 7.
Distancia entre GC y GE en las covariables y sus interacciones
Dado que las distribuciones de GE y GC son iguales en cuanto a las covariables, resulta pertinente analizar los efectos causales de la diferencia del rendimiento entre ambos grupos (tabla 3). Mientras que sin aplicar PSM se observan diferencias significativas favorables a los estudiantes que cursan más tiempo EI con tamaños del efecto medios, en la muestra emparejada por PSM se mantienen las diferencias significativas pero de inferior magnitud. De hecho, la diferencia de medias entre ambos grupos pasa de algo más de 50 puntos en la muestra inicial a algo menos de 20 en la muestra emparejada.
| Media GC | Media GE | t | p. | d | |
| Muestra iniciala | 450.32 | 500.35 | 17.26 | <.001 | 0.587 |
| Muestra emparejada PSMb | 450.32 | 470.11 | 5.25 | <.001 | 0.176 |
Por tanto, tras seleccionar sujetos del GC realmente comparables a sus pares del GE mediante el método PSM, suponiendo que se han incluido todas las covariables clave, se puede afirmar que existe una relación causa-efecto directa, con tamaños del efecto pequeños, entre la escolarización en educación infantil y el rendimiento académico del estudiante cuando tiene 15 años.
IV – Efecto causal de las expectativas académicas sobre el rendimiento
La figura 8 muestra la distribución de las variables rendimiento en matemáticas (Y) y expectativas académicas del estudiante (X). La mayor parte de los estudiantes (62%) declaran querer alcanzar estudios universitarios, mientras que una mínima parte (3.1%) indican que únicamente quieren alcanzar el nivel de educación secundaria obligatoria.
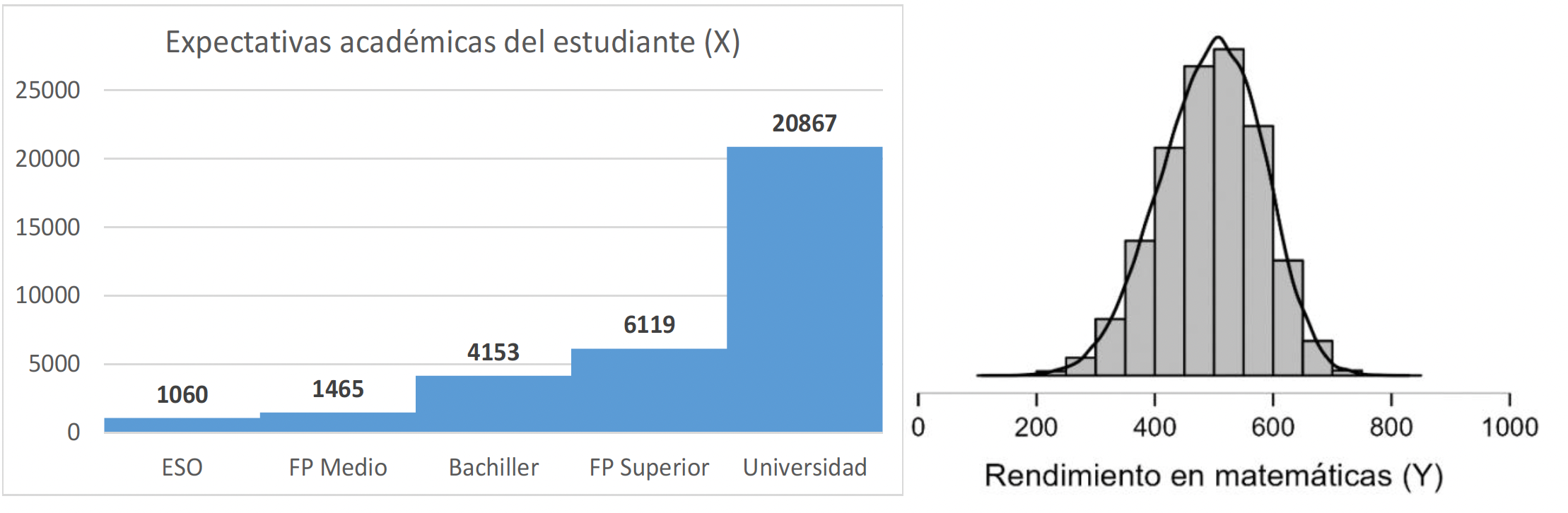
Figura 8.
Distribución del rendimiento en matemáticas (Y) y las expectativas (X)
El cumplimiento de los supuestos previos del modelo IV se presenta en la tabla 4. En primer lugar, se observa que existe endogeneidad, al rechazarse la H0 en el test de Wu-Hausman. Las evidencias también muestran que el instrumento es fuerte (rechazo la H0 de instrumentos débiles y F > 10) y que tiene una correlación significativa de intensidad alta con la variable X, por lo que se puede considerar relevante.
| Estadístico | p. | F | ||
| Wu-Hausman (Endogeneidad) | 2093 | <.001 | - | |
| Relevancia | Instrumentos débiles | 3416 | <.001 | 4084.97 |
| Correlación (rxz) | .414 | <.001 | - | |
La tabla 5 presenta los modelos de regresión MCO e IV (estimación 2SLS) obtenidos. Se observa que, tras controlar las expectativas académicas del estudiante con el NSE familiar del mismo, los efectos directos de X sobre Y aumentan de manera clara. Un aumento de una unidad en X supone aumentar el rendimiento en más de 86 puntos en el modelo IV, mientras que en el modelo MCO solo aumenta 34 puntos.
| MCO | IV (2SLS) | |||||||
| b | ET | t | p. | b | ET | t | p. | |
| Intercepto | 347.97 | 1.81 | 192.51 | <.001 | 121.18 | 7.00 | 17.31 | <.001 |
| Expectativa académica | 33.95 | 0.41 | 83.40 | <.001 | 86.51 | 1.60 | 54.24 | <.001 |
Este cambio en el peso de las expectativas académicas de un modelo a otro se observa mejor en la figura 9. A pesar de que el intervalo de confianza alrededor del parámetro es más amplio en IV debido al aumento en el error típico, la influencia directa de las expectativas del estudiante sobre el rendimiento es claramente superior. Un punto de aumento en las expectativas académicas del estudiante supone en el modelo IV un aumento de casi 87 puntos en el rendimiento, mientras que en el modelo MCO suponía un aumento de 34 puntos.

Figura 9.
Parámetro asociado a las expectativas del estudiante en modelos IV y MCO
En conclusión, considerando que se ha establecido un control adecuado de la endogeneidad (el NSE familiar es una variable causa tanto de las expectativas académicas como del rendimiento del estudiante), el modelo IV apunta a que el efecto causal de las expectativas académicas sobre el rendimiento es directo y significativo, incluso de intensidad más elevada a lo indicado en el modelo correlacional MCO.
RDD – Efecto causal de la escolarización en escuelas urbanas VS rurales sobre el rendimiento
La figura 10 muestra la distribución de escuelas por NSE en función del tamaño del municipio. Se observa una relación intensa entre ambas variables: mientras que la distribución del NSE en las escuelas rurales es muy homogénea y está en general en puntuaciones inferiores a 0, en las grandes urbes encontramos más dispersión y valores NSE superiores. Aplicando la prueba de . para muestras independientes nos encontramos con diferencias significativas con un tamaño del efecto muy alto (t = 6.19, p < .001, d = 1.23).
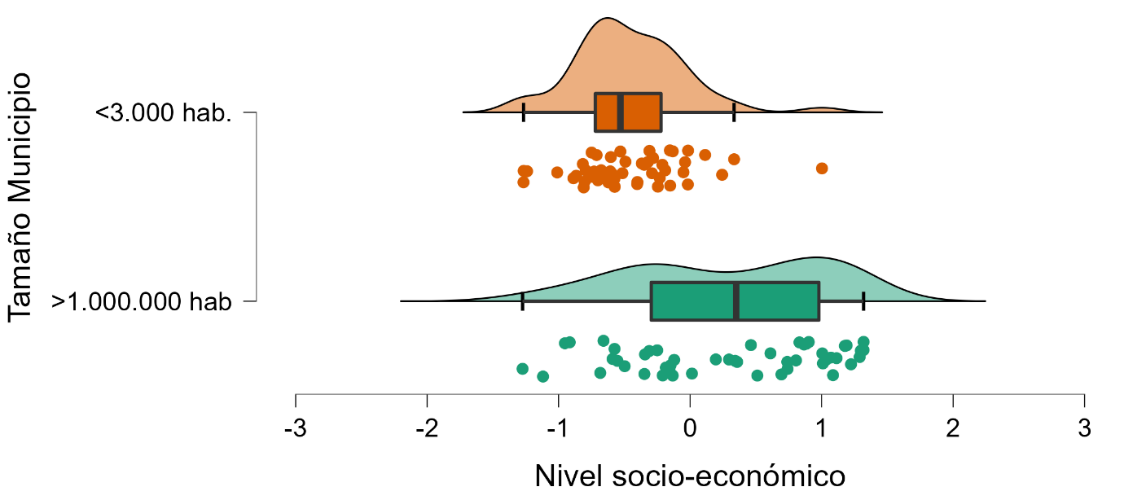
Figura 10.
Distribución por NSE de escuelas rurales y de grandes urbes
Por otro lado, también se encuentra una relación significativa con tamaño del efecto moderado entre el rendimiento y el tamaño del municipio (t = 2.43, p = .017, d = .49), aunque podemos plantearnos si esos efectos se deben a la relación espuria que ejerce el NSE (figura 11). Aplicando el modelo de regresión con tamaño del municipio y NSE como variables predictoras, el parámetro b de tamaño del municipio sigue resultando significativo (b = 18.96, t = 2.82, p = .006), igual que el de NSE (b = 53.72, t = 11.25, p < .001)
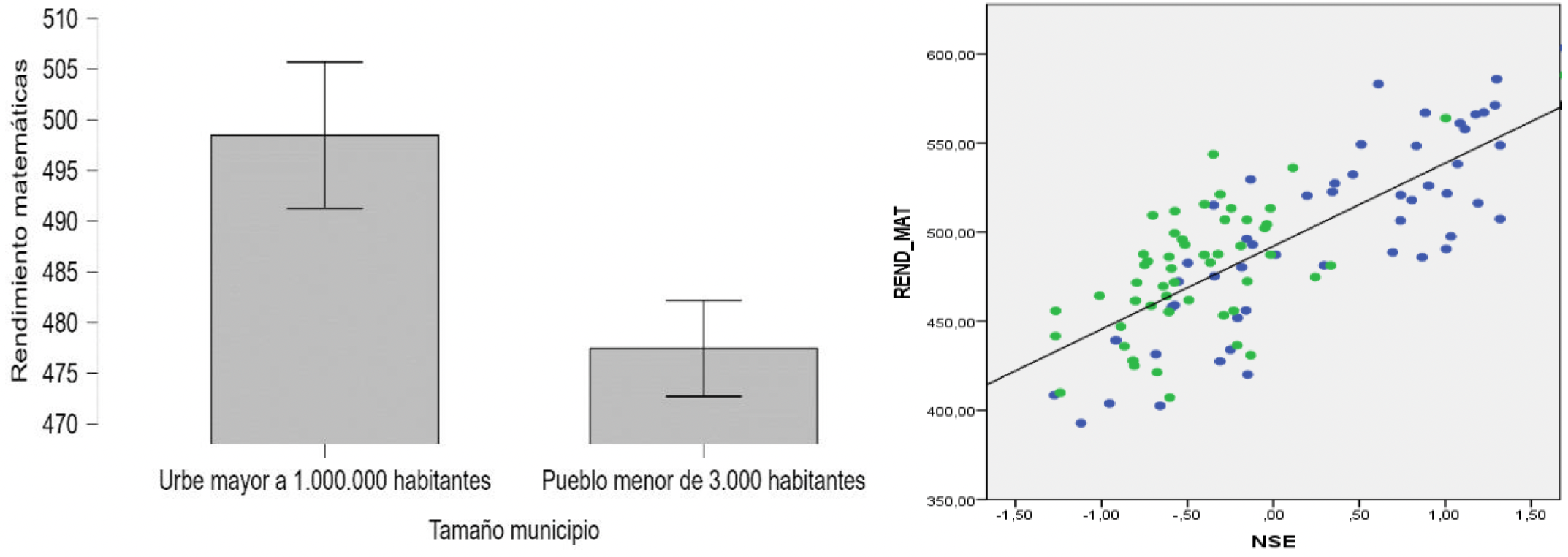
Figura 11.
Rendimiento en matemáticas por tamaño de escuela y NSE
Así, podemos afirmar que existe una relación lineal entre el tamaño del municipio y el rendimiento, incluso controlando por NSE. La cuestión ahora es: ¿existe un efecto causal del tamaño de la localidad (gran urbe VS pueblo) sobre el rendimiento en matemáticas?
Dado que existe una asociación muy intensa entre el NSE y el tamaño de la localidad, la técnica RDD difusa parece una buena elección. El modelo incluirá NSE como variable X, el tamaño del municipio como variable T y el rendimiento como variable Y.
En primer lugar, se establecen los valores k y h. Dada la distribución del NSE observada en ambos grupos en las figuras 8 y 9, consideramos adecuado establecer el punto de corte k = 0. La tabla 6 muestra el cumplimiento del supuesto de continuidad de la variable NSE, y el valor h estimado para k = 0. Se acepta la hipótesis nula de continuidad alrededor del valor 0 y se establece el rango de puntuaciones de NSE (-.741, .741), por lo que es adecuado aplicar RDD. Se aplicará el modelo en los 66 centros educativos que están dentro de ese rango de puntuaciones.
La tabla 7 muestra los resultados obtenidos en ambos pasos del modelo de regresión RDD. Se observa que el efecto medio del tratamiento no es significativo ( 1 = -32.10, p = .801).
| Test McCrary (k=0) | Punto de corte h (Imbens-Kalyanaraman) | |
| Z | p | |
| -1.917 | .055 | h =.741 |
| Primer paso | Segundo paso | |||||||
| b | ET | t | p | g | ET | t | p | |
| Intercepto | 0.631 | 0.12 | 5.24 | <.001 | 508.06 | 76.57 | 6.64 | <.001 |
| D (dummy trat.) | -0.170 | 0.28 | -0.60 | .550 | - | - | - | - |
| (instrumento) | - | - | - | - | -32.10 | 126.86 | -0.25 | .801 |
| NSE | -0.047 | 0.391 | -0.12 | .905 | 25.61 | 32.44 | 0.79 | .433 |
| D*NSE | -0.534 | 0.84 | -0.63 | .529 | 47.30 | 124.13 | 0.38 | .704 |
Suponiendo un control adecuado de la endogeneidad en RDD, podemos concluir que el tamaño del municipio no ejerce efectos causales sobre el rendimiento de los estudiantes. Estos resultados contrastan con los obtenidos con el enfoque correlacional-inferencial, que encuentra efectos significativos en la relación entre ambas variables incluso controlando por el NSE.
Discusión y conclusiones
Investigadores de referencia en estadística multivariante enfatizan el potencial de las técnicas de inferencia causal para probar efectos causales en muestras ex post facto (e.g., Imbens & Rubin, 2015; Rosenbaum & Rubin, 2022), de hecho, autores en esta línea de investigación recibieron el premio Nobel en Economía[3] del año 2021. Además, desde hace unos años autores internacionales del campo educativo hacen hincapié en la utilización de estas técnicas en las evaluaciones educativas a gran escala (e.g., Kaplan, 2016; Rutkowski & Delandshere, 2016). Dado el limitado impacto que actualmente tienen estas técnicas en investigación educativa, nuestro objetivo ha sido mostrar las posibilidades de la inferencia causal para analizar datos de panel, concretamente con la muestra española de PISA 2018.
En relación al PSM, los resultados muestran que se seleccionaron covariables clave para controlar la endogeneidad (Rosenbaum & Rubin, 2022). El empleo de datos de la evaluación PISA (OECD, 2019), permitió esta selección exhaustiva de covariables y la obtención de grupos tratamiento y control realmente comparables. Los resultados obtenidos confirman la primera hipótesis planteada en este trabajo (H1): la asistencia a educación infantil ejerce un efecto causal sobre el rendimiento de los estudiantes españoles durante la educación secundaria. Mientras que revisiones sistemáticas y meta-análisis internacionales apuntan hacia este resultado (Barnett, 1998; McCoy et al., 2017), algunos estudios previos con muestras regionales de tamaño más reducido obtuvieron conclusiones similares en otros países empleando también PSM (Amadon et al., 2022; Barnett & Jung, 2021; Courtney et al., 2023).
El empleo de IV incluyó como instrumento para el control de la endogeneidad la variable NSE, covariable fundamental en los estudios sobre factores asociados al rendimiento (Gamazo & Martínez-Abad, 2020; Martínez-Abad et al., 2020). Mientras que estudios previos de carácter correlacional y multivariante ya observan relaciones directas y significativas entre las expectativas y el rendimiento en la educación secundaria (Levi et al., 2014; Sanders et al., 2001; Suárez-Álvarez et al., 2014), nuestros resultados confirman que esta relación es de carácter causal (H2), observando efectos causales significativos incluso superiores a los esperados: los efectos de las expectativas académicas obtenidos en el IV resultaron superiores a los obtenidos con MCO, apuntando al sesgo asociado a atribuir causalidad a partir de modelos de regresión en una etapa.
En respuesta a la H3, la técnica RDD se aplicó para estimar los efectos del tipo de escuela rural-urbana (tratamiento) sobre el rendimiento (variable Y) de estudiantes españoles, teniendo en cuenta la relación estrecha del NSE (covariable X) con el tipo de escuela. Los resultados obtenidos apuntan de nuevo al sesgo asociado al uso de la regresión MCO: incluso incluyendo el NSE como covariable en el modelo MCO, los efectos del tipo de escuela obtenidos en RDD son significativamente diferentes. Estudios previos de carácter correlacional en otros países ya apuntaban en esta dirección (Amini & Nivorozhkin, 2015; Song & Tan, 2022).
Dado el carácter didáctico de este trabajo, su principal limitación se encuentra en que se han presentado ejemplos de aplicación simples, sin añadir en los modelos otras covariables para el control de la covarianza. No debemos olvidar la naturaleza compleja y multivariada de la realidad educativa, lo que en ocasiones requiere del empleo de modelos más amplios y comprensivos que los aquí presentados. Así, consideramos de interés que investigaciones futuras se centren de manera específica en cada una de las técnicas estudiadas. Esto permitirá abordar más en profundidad las posibilidades concretas que ofrece cada técnica y explorar la construcción de modelos estadísticos más complejos y, por ende, comprensivos.
Tal y como se ha presentado en este trabajo, las técnicas de inferencia causal no son excesivamente complejas a nivel conceptual o técnico. Igualmente, hemos mostrado que su implementación en investigación aplicada es simple a través del empleo de paquetes estadísticos de libre disposición. Por todo ello, entendemos que el uso marginal del conjunto de técnicas de inferencia causal por parte del investigador aplicado de ciencias de la educación se debe a su profundo desconocimiento. Así, este trabajo presenta ejemplos concretos y simples de aplicación de las tres principales técnicas de inferencia causal (PSM, IV y RDD) con la intención de que sean fácilmente replicables y transferibles por otros investigadores en sus estudios no experimentales.
Materiales suplementarios
Apéndice. (pdf)
Agradecimientos
Proyecto PID2021-125775NB-I00 financiado por MCIN/AEI/10.13039/501100011033/ y por FEDER Una manera de hacer Europa.
Referencias
Ali, M. S., Groenwold, R. H. H., Pestman, W. R., Belitser, S. V., Roes, K. C. B., Hoes, A. W., de Boer, A., & Klungel, O. H. (2014). Propensity score balance measures in pharmacoepidemiology: A simulation study. Pharmacoepidemiology and Drug Safety, 23(8), 802-811. https://doi.org/10.1002/pds.3574
Altman, M. (2020). A more scientific approach to applied economics: Reconstructing statistical, analytical significance, and correlation analysis. Economic Analysis and Policy, 66, 315-324. https://doi.org/10.1016/j.eap.2020.05.006
Amadon, S., Gormley, W. T., Claessens, A., Magnuson, K., Hummel-Price, D., & Romm, K. (2022). Does early childhood education help to improve high school outcomes? Results from Tulsa. Child Development, 93(4), e379-e395. https://doi.org/10.1111/cdev.13752Amini, C., & Nivorozhkin, E. (2015). The urban–rural divide in educational outcomes: Evidence from Russia. International Journal of Educational Development, 44, 118-133. https://doi.org/10.1016/j.ijedudev.2015.07.006
Amini, C., & Nivorozhkin, E. (2015). The urban–rural divide in educational outcomes: Evidence from Russia. International Journal of Educational Development, 44, 118-133. https://doi.org/10.1016/j.ijedudev.2015.07.006
Angrist, J. D., Imbens, G. W., & Rubin, D. B. (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association, 91(434), 444-455. https://doi.org/10.1080/01621459.1996.10476902
Antonakis, J., Bendahan, S., Jacquart, P., & Lalive, R. (2010). On making causal claims: A review and recommendations. The Leadership Quarterly, 21(6), 1086-1120. https://doi.org/10.1016/j.leaqua.2010.10.010
Austin, P. C. (2011). Comparing paired vs non-paired statistical methods of analyses when making inferences about absolute risk reductions in propensity-score matched samples. Statistics in Medicine, 30(11), 1292-1301. https://doi.org/10.1002/sim.4200
Barnett, W. S. (1998). Long-Term Cognitive and Academic Effects of Early Childhood Education on Children in Poverty. Preventive Medicine, 27(2), 204-207. https://doi.org/10.1006/pmed.1998.0275
Barnett, W. S., & Jung, K. (2021). Effects of New Jersey’s Abbott preschool program on children’s achievement, grade retention, and special education through tenth grade. Early Childhood Research Quarterly, 56, 248-259. https://doi.org/10.1016/j.ecresq.2021.04.001
Belitser, S. V., Martens, E. P., Pestman, W. R., Groenwold, R. H. H., de Boer, A., & Klungel, O. H. (2011). Measuring balance and model selection in propensity score methods. Pharmacoepidemiology and Drug Safety, 20(11), 1115-1129. https://doi.org/10.1002/pds.2188
Campbell, D. T., & Stanley, J. (1963). Experimental and quasi-experimental designs for research. Wadsworth Publishing.
Castro Aristizabal, G., Giménez, G., & Pérez Ximénez-De-Embún, D. (2017). Educational inequalities in latin ethod, PISA 2012: Causes of differences in school performance between public and private schools. Revista de Educacion, 2017(376), 33-59. Scopus. https://doi.org/10.4438/1988-592X-RE-2017-376-343
Choi, A., Calero, J., & Escardíbul, J.-O. (2012). Private tutoring and academic achievement in Korea: An approach through PISA-2006. KEDI Journal of Educational Policy, 9(2), 299-322. Scopus.
Cinelli, C., Forney, A., & Pearl, J. (2022). A crash course in good and bad controls. Sociological Methods & Research, 00491241221099552. https://doi.org/10.1177/00491241221099552
Cordero, J. M., & Gil-Izquierdo, M. (2018). The effect of teaching strategies on student achievement: An analysis using TALIS-PISA-link. Journal of Policy Modeling, 40(6), 1313-1331. Scopus. https://doi.org/10.1016/j.jpolmod.2018.04.003
Courtney, J. R., Garcia, J. T., Rowberry, J., Eckberg, N., Dinces, S. M., Lobaugh, C. S., & Tolman, R. T. (2023). Measuring impact of New Mexico prekindergarten on standardized test scores and high school graduation using propensity score matching. International Journal of Child Care and Education Policy, 17(1), 9. https://doi.org/10.1186/s40723-023-00112-9
Crespo-Cebada, E., Pedraja-Chaparro, F., & Santín, D. (2014). Does school ownership matter? An unbiased efficiency comparison for regions of Spain. Journal of Productivity Analysis, 41(1), 153-172. Scopus. https://doi.org/10.1007/s11123-013-0338-y
Gamazo, A., & Martínez-Abad, F. (2020). An Exploration of Factors Linked to Academic Performance in PISA 2018 Through Data Mining Techniques. Frontiers in Psychology, 11. https://doi.org/10.3389/fpsyg.2020.575167
García-Pérez, J.I., & Hidalgo-Hidalgo, M. (2017). No student left behind? Evidence from the Programme for School Guidance in Spain. Economics of Education Review, 60, 97-111. Scopus. https://doi.org/10.1016/j.econedurev.2017.08.006
Hill, A. D., Johnson, S. G., Greco, L. M., O’Boyle, E. H., & Walter, S. L. (2021). Endogeneity: A Review and agenda for the methodology-practice divide affecting micro and macro research. Journal of Management, 47(1), 105-143. https://doi.org/10.1177/0149206320960533
Huenermund, P., Louw, B., & Rönkkö, M. (2022). The choice of control variables: How causal graphs can inform the decision. Academy of Management Proceedings, 2022(1), 15534. https://doi.org/10.5465/AMBPP.2022.294
Imai, K., Keele, L., Tingley, D., & Yamamoto, T. (2011). Unpacking the black box of causality: Learning about causal mechanisms from experimental and observational studies. American Political Science Review, 105(4), 765-789. https://doi.org/10.1017/S0003055411000414
Imbens, G. W., & Kalyanaraman, K. (2012). Optimal bandwidth choice for the regression discontinuity estimator. Review of Economic Studies, 79(3), 933-959. Scopus. https://doi.org/10.1093/restud/rdr043
Imbens, G. W., & Lemieux, T. (2008). Regression discontinuity designs: A guide to practice. Journal of Econometrics, 142(2), 615-635. Scopus. https://doi.org/10.1016/j.jeconom.2007.05.001
Imbens, G. W., & Rubin, D. B. (2015). Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction.
Jin, S. (2022). On inconsistency of the overidentification test for the model-implied instrumental variable approach. Structural Equation Modeling. Scopus. https://doi.org/10.1080/10705511.2022.2122978
Kaplan, D. (2016). Causal inference with large-scale assessments in education from a Bayesian perspective: A review and synthesis. Large-Scale Assessments in Education, 4(1). Scopus. https://doi.org/10.1186/s40536-016-0022-6
Kerlinger, F. N., & Lee, H. (1999). Foundations of behavioral research (004 ed.). Wadsworth Publishing.
Lee, D. S., & Lemieux, T. (2010). Regression discontinuity designs in economics. Journal of Economic Literature, 48(2), 281-355. Scopus. https://doi.org/10.1257/jel.48.2.281
Levi, U., Einav, M., Ziv, O., Raskind, I., & Margalit, M. (2014). Academic expectations and actual achievements: The roles of hope and effort. European Journal of Psychology of Education, 29(3), 367-386. https://doi.org/10.1007/s10212-013-0203-4
Lopez-Agudo, L. A., González-Betancor, S. M., & Marcenaro-Gutierrez, O. D. (2021). Language at home and academic performance: The case of Spain. Economic Analysis and Policy, 69, 16-33. Scopus. https://doi.org/10.1016/j.eap.2020.11.003
Maydeu-Olivares, A., Shi, D., & Fairchild, A. J. (2020). Estimating causal effects in linear regression models with observational data: The instrumental variables regression model. Psychological Methods, 25(2), 243-258. https://doi.org/10.1037/met0000226
Martínez-Abad, F., Gamazo, A., & Rodríguez-Conde, M.-J. (2020). Educational Data Mining: Identification of factors associated with school effectiveness in PISA assessment. Studies in Educational Evaluation, 66, 100875. https://doi.org/10.1016/j.stueduc.2020.100875
McCoy, D. C., Yoshikawa, H., Ziol-Guest, K. M., Duncan, G. J., Schindler, H. S., Magnuson, K., Yang, R., Koepp, A., & Shonkoff, J. P. (2017). Impacts of Early Childhood Education on Medium- and Long-Term Educational Outcomes. Educational Researcher, 46(8), 474-487. https://doi.org/10.3102/0013189X17737739
McCrary, J. (2008). Manipulation of the running variable in the regression discontinuity design: A density test. Journal of Econometrics, 142(2), 698-714. https://doi.org/10.1016/j.jeconom.2007.05.005
OECD. (2009). PISA Data Analysis Manual: SPSS, Second Edition. Organisation for Economic Co-operation and Development. https://doi.org/10.1787/19963777
OECD. (2019). PISA 2018 Assessment and Analytical Framework. OECD Publishing. https://doi.org/10.1787/b25efab8-en
Pearl, J., & Mackenzie, D. (2018). The book of why: The new science of cause and effect. Falta editorial
Pokropek, A. (2016). Introduction to instrumental variables and their application to large-scale assessment data. Large-Scale Assessments in Education, 4(1). https://doi.org/10.1186/s40536-016-0018-2
Rosenbaum, P. R., & Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41-55. https://doi.org/10.2307/2335942
Rosenbaum, P. R., & Rubin, D. B. (2022). Propensity scores in the design of observational studies for causal effects. Biometrika, asac054. https://doi.org/10.1093/biomet/asac054
Rubin, D. B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology, 66, 688-701. https://doi.org/10.1037/h0037350
Rutkowski, D., & Delandshere, G. (2016). Causal inferences with large scale assessment data: Using a validity framework. Large-scale Assessments in Education, 4(1), 6. https://doi.org/10.1186/s40536-016-0019-1
Sanders, C. E., Field, T. M., & Diego, M. A. (2001). Adolescents’ academic expectations and achievement. Adolescence, 36(144), 795-802.
Song, Q., & Tan, C. Y. (2022). The association between family socioeconomic status and urban–rural and high-school attainment gaps: A logistic regression analysis of the China Family Panel Studies data. British Educational Research Journal, 48(6), 1102-1124. https://doi.org/10.1002/berj.3817
Stock, J., & Yogo, M. (2005). Testing for weak instruments in linear iv regression. En D. W. K. Andrews, Identification and Inference for Econometric Models (pp. 80-108). Cambridge University Press.
Suárez-Álvarez, J., Fernández-Alonso, R., & Muñiz, J. (2014). Self-concept, motivation, expectations, and socioeconomic level as predictors of academic performance in mathematics. Learning and Individual Differences, 30, 118-123. https://doi.org/10.1016/j.lindif.2013.10.019
Wooldridge, J. M. (2010). Econometric analysis of cross section and panel data, second edition. Revisar
Zhang, Z., Kim, H. J., Lonjon, G., & Zhu, Y. (2019). Balance diagnostics after propensity score matching. Annals of Translational Medicine, 7(1), 16. https://doi.org/10.21037/atm.2018.12.10
Notas de autor
fma@usal.es
Enlace alternativo
https://revistaseug.ugr.es/index.php/RELIEVE/article/view/26843 (html)
